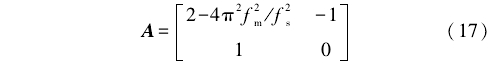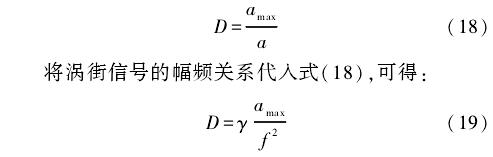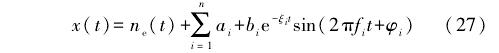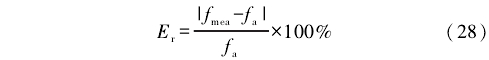|
爾曼濾(lü)波渦街(jie)流量計(jì)信号處(chu)理方法(fǎ)
|
摘要:爲(wei)了改善(shàn)渦街流(liú)量計
的(de)性能,提(ti)出了一(yi)種基于(yú)卡爾曼(màn)濾波的(de)渦街信(xìn)号處理(lǐ)方法。根(gen)據渦街(jiē)信号的(de)特點,設(shè)計了一(yi)個線性(xìng)渦街信(xin)号模型(xíng)。結合模(mó)糊搜索(suǒ)和叠代(dai)算法,通(tong)過分析(xi)卡爾曼(màn)濾波器(qi)算法的(de)原理和(hé)關鍵參(cān)數,改進(jin)卡爾曼(màn)濾波器(qi)算法。通(tōng)過仿真(zhēn)模拟和(he)實際流(liu)量實驗(yàn)驗證了(le)所提出(chu)的方法(fǎ),并與其(qí)他方法(fa)進行了(le)比較。實(shi)驗結果(guo)表明,所(suo)提出的(de)方法具(ju)有自适(shi)應濾波(bo)、抗幹擾(rǎo)能力和(he)濾波速(su)度的優(yōu)點。
0引言(yan)
渦街流(liú)量計作(zuò)爲一種(zhong)振動型(xing)流量計(ji),具有應(ying)用範圍(wéi)廣、測量(liang)介質多(duo)耐高溫(wen)、耐高壓(yā)等優點(dian),具有廣(guang)闊的發(fa)展前景(jing)。渦街流(liu)量計利(li)用流體(ti)振動的(de)原理來(lai)測量流(liú)量。當流(liu)體通過(guo)一個垂(chuí)直放置(zhi)的非流(liu)線型旋(xuán)渦發生(shēng)體時,發(fa)生體兩(liang)側會産(chǎn)生兩排(pái)交錯排(pai)列的旋(xuan)渦,被稱(cheng)爲卡門(mén)渦街,如(rú)圖1所示(shi)。發生體(tǐ)後方的(de)應力型(xing)壓電傳(chuán)感器将(jiāng)旋渦産(chǎn)生的壓(ya)力差轉(zhuan)換爲電(diàn)荷信号(hào)。電荷信(xìn)号的變(bian)化頻率(lü)與旋渦(wō)的産生(sheng)頻率-緻(zhì)。
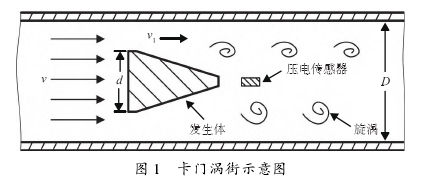
渦街信(xin)号具有(you)以下兩(liang)個特點(dian)。
1)壓電傳(chuan)感器輸(shū)出的電(diàn)荷信号(hào)QH滿足正(zhèng)弦規律(lü),如式(1)所(suǒ)示
QH=γρƒ2sin(2πƒt+φa)(1)
式中(zhōng):γ爲壓電(diàn)傳感器(qi)的系數(shù),ρ爲流體(ti)密度,ƒ爲(wei)渦街頻(pín)率,φa爲初(chu)始相位(wei)。
2)在渦街(jie)流量計(jì)中,電荷(hé)放大器(qi)一般用(yòng)于将傳(chuan)感器輸(shū)出的電(diàn)荷信号(hào)轉換成(chéng)電壓信(xìn)号。電壓(yā)信号是(shì)待處理(li)的原始(shǐ)信号,和(he)電荷信(xìn)号一樣(yàng)爲正弦(xian)波形式(shi)。當流體(ti)密度和(he)發生體(ti)的寬度(du)爲固定(dìng)值時,渦(wō)街信号(hao)的幅值(zhi)與頻率(lǜ)的平方(fang)成正比(bi),如式(2)所(suǒ)示
α∞ƒ2(2)
式中(zhong):α爲渦街(jiē)信号的(de)幅值。
由(yóu)于渦街(jiē)流量計(jì)的傳感(gan)器屬于(yú)振動型(xing)傳感器(qi),很容易(yi)受到振(zhen)動幹擾(rao),這對渦(wō)街流量(liàng)計的測(ce)量精度(du)和測量(liàng)範圍有(yǒu)很大的(de)影響。由(yóu)于渦街(jiē)信号的(de)幅值與(yu)頻率的(de)平方成(chéng)正比,在(zài)高流速(su)下信号(hao)的信噪(zao)比大,信(xin)号受噪(zao)聲影響(xiǎng)小;在低(di)流速下(xià)信号的(de)信噪比(bi)小,信号(hao)受噪聲(sheng)影響大(da),增加了(le)信号檢(jiǎn)測的難(nán)度。國内(nei)外衆多(duō)學者對(dui)這一問(wen)題進行(háng)了研究(jiu)(2-3]。近年來(lai),卡爾曼(man)濾波方(fāng)法也開(kāi)始被應(ying)用在渦(wo)街流量(liàng)計的信(xin)号處理(lǐ)中。
卡爾(er)曼濾波(bo)是科學(xue)家R.E.Kalman等在(zài)1960年提出(chū)的一種(zhong)适用于(yú)離散随(sui)機非平(píng)穩系統(tǒng)的最優(yōu)估計算(suàn)法。它基(jī)于線性(xìng)離散系(xi)統,将最(zui)優濾波(bo)理論與(yu)狀态空(kong)間思想(xiang)相結合(hé)。宋開臣(chén)等[4]針對(dui)壓電式(shì)渦街流(liú)量計抗(kang)幹擾性(xing)差的缺(que)點,提出(chu)了基于(yu)多傳感(gǎn)器融合(hé)的渦街(jiē)信号檢(jian)測方法(fǎ)。該方法(fa)通過無(wu)迹卡爾(er)曼濾波(bo)算法将(jiang)壓差傳(chuan)感器測(ce)量的鈍(dun)體前後(hou)壓差和(hé)其下遊(yóu)的渦街(jiē)信号頻(pín)率進行(háng)融合,增(zeng)強了壓(yā)電式渦(wo)街流量(liang)計的抗(kang)振能力(lì),有效提(tí)高了數(shu)字帶通(tōng)濾波器(qì)的測量(liàng)精度。Shao等(deng)[5]針對渦(wo)街流量(liàng)計提出(chū)了一種(zhong)基于分(fen)段卡爾(er)曼濾波(bo)的數字(zi)信号處(chu)理方法(fǎ)。該方法(fa)首先分(fen)析瞬态(tai)沖擊的(de)特性,建(jian)立數學(xue)模型,然(rán)後在流(liú)量信号(hào)數據中(zhōng)找到含(han)有強瞬(shùn)态沖擊(jī)的數據(jù)段,并對(duì)數據段(duan)進行卡(ka)爾曼濾(lǜ)波,以降(jiang)低瞬态(tai)沖擊的(de)功率。
本(běn)文提出(chu)了一種(zhǒng)基于渦(wo)街信号(hao)模型的(de)卡爾曼(màn)濾波的(de)信号處(chu)理方法(fa)(以下簡(jiǎn)稱“本方(fang)法")。首先(xian),根據微(wēi)分原理(lǐ)和線性(xìng)矩陣對(dui)非線性(xing)的渦街(jie)信号進(jìn)行線性(xìng)化處理(lǐ)并建立(lì)模型;其(qi)次,根據(ju)渦街信(xìn)号的幅(fu)頻關系(xì),初始化(huà)渦街信(xin)号模型(xing)頻率;再(zài)次,将濾(lǜ)波後的(de)輸出頻(pin)率作爲(wei)下一個(gè)循環的(de)初始渦(wō)街模型(xíng)頻率進(jìn)行叠代(dai)和模糊(hú)搜索,直(zhí)到輸出(chū)頻率與(yu)模型頻(pín)率的誤(wu)差在渦(wo)街流量(liàng)計允許(xǔ)的誤差(chà)範圍内(nèi)爲止;最(zui)後,通過(guò)仿真實(shí)驗和實(shi)流實驗(yan)對該方(fang)法進行(háng)了驗證(zhèng)。
1卡爾曼(màn)濾波原(yuán)理和渦(wo)街系統(tǒng)模型
1.1卡(ka)爾曼濾(lü)波原理(lǐ)
卡爾曼(màn)濾波是(shi)一種利(lì)用線性(xing)系統狀(zhuang)态方程(cheng),通過系(xi)統輸人(rén)的觀測(ce)數據對(dui)系統狀(zhuang)态進行(hang)最優估(gū)計的算(suàn)法。其基(ji)本原理(li)如下:假(jia)設有一(yi)個離散(sàn)的線性(xing)系統Xk,通(tong)過k-1時刻(ke)的最優(you)估計Xk-1得(dé)到k時刻(kè)的預測(ce)值Xk|k-1,并用(yòng)k時刻的(de)觀測值(zhí)Zk修正預(yu)測值,從(cóng)而得到(dao)h時刻的(de)最優估(gu)計Xk。圖2顯(xiǎn)示了卡(kǎ)爾曼濾(lü)波原理(lǐ)。
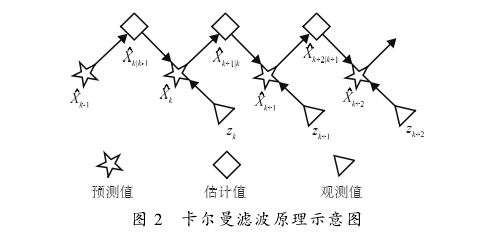
對于沒(mei)有控制(zhi)輸人的(de)系統,卡(ka)爾曼濾(lü)波算法(fǎ)的狀态(tài)方程和(he)觀測方(fang)程可用(yòng)式(3).式(4)表(biǎo)示
Xk+1=AXk+Bwk(3)
Yk+1=HXk+1+Dʋk+1(4)
式中(zhong):Xk爲n維的(de)狀态變(bian)量在k時(shi)刻的值(zhí),wk爲p維的(de)過程噪(zào)聲,Yk+1爲m維(wei)的觀測(cè)變量,ʋk+1爲(wei)m維的觀(guan)測噪聲(shēng),A爲變量(liang)Xk的狀态(tài)轉移矩(jǔ)陣,H爲系(xi)統參數(shu)矩陣,B爲(wei)過程噪(zao)聲的系(xì)數矩陣(zhèn),D爲觀測(cè)噪聲的(de)系數.矩(jǔ)陣。wk和ʋk+1是(shi)均值爲(wèi)0且互不(bu)相關的(de)高斯白(bái)噪聲。不(bú)難看出(chu),由式(3)和(hé)式(4)構建(jian)的系統(tong)模型不(bu)包含渦(wo)街信号(hao)的特征(zheng)。
1.2渦街系(xì)統模型(xing)
由于渦(wō)街信号(hào)是非線(xiàn)性正弦(xián)波信号(hào),不滿足(zú)卡爾曼(màn)濾波系(xì)統模型(xíng)的線性(xing)要求,不(bú)能成爲(wèi)卡爾曼(màn)濾波算(suan)法的系(xì)統模型(xíng),需要利(li)用微分(fen)原理和(he)線性矩(jǔ)陣對渦(wō)旋信号(hào)進行線(xian)性化處(chù)理,具體(ti)推導過(guò)程如下(xià)。
假設,渦(wō)街信号(hao)的數學(xue)模型如(rú)式(5)所示(shì):
s(t)=asin(2πƒt)(5)
那麽,其(qi)二階導(dao)數可以(yi)用式(6)表(biǎo)示:
s"(t)=-4π2aƒ2sin(2πƒt)(6)
将式(shì)(5)代人式(shi)(6),得到式(shi)(7):
s"(1)=-4π2ƒ2s(t)(7)
根據導(dao)數的定(dìng)義,當t>△t且(qie)△t→0時,可得(dé)式(8):

2算法(fa)實現
2.1算(suàn)法設計(ji)
卡爾曼(màn)濾波是(shì)用觀測(ce)量(實際(jì)信号)對(dui)預測變(biàn)量(模型(xíng)信号)進(jin)行修正(zheng),濾波結(jie)果介于(yú)實際信(xin)号和模(mó)型信号(hao)之間。同(tóng)樣,濾波(bō)後的信(xìn)号頻率(lǜ)也介于(yú)實際信(xin)号頻率(lü)和模型(xing)信号頻(pín)率之間(jiān)。爲此,設(she)計了一(yī)種基于(yu)渦街模(mo)型的卡(ka)爾曼濾(lǜ)波算法(fa),以叠代(dài)的方法(fǎ)搜索渦(wō)街信号(hao)的頻率(lǜ)。
首先,根(gēn)據渦街(jie)信号的(de)幅頻關(guān)系設置(zhi)初始系(xì)統模型(xíng)頻率。按(an)照式(2)對(dui)液體介(jie)質管道(dào)上采集(jí)到的渦(wō)流信号(hao)的幅值(zhí)和頻率(lǜ)進行二(èr)次多項(xiang)式拟合(he),得到在(zai)液體介(jie)質中50mm口(kǒu)徑渦街(jiē)流量計(jì)信号的(de)幅值和(he)頻率的(de)關系,如(rú)式(15)所示(shì)。
α=1.789x10-5ƒ2(15)
同理,對(duì)采集到(dào)的氣體(ti)數據進(jin)行拟合(hé),可以得(dé)到氣體(ti)信号的(de)幅值與(yǔ)頻率的(de)關系,如(rú)式(16)所示(shì)
α=2.622x10-8ƒ2(16)
用ƒm表示(shì)狀态模(mo)型頻率(lü),用ƒmax,表示(shi)渦街信(xin)号的最(zuì)大頻率(lǜ),令ƒm=ƒmax。這樣(yàng)設置的(de)目的是(shi)減少叠(die)代次數(shu)和計算(suan)量。于是(shì),式(3)中的(de)系數矩(jǔ)陣A可用(yòng)式(17)表示(shi)。
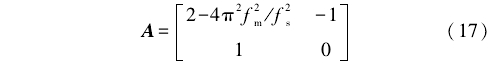
當流速(sù)低時,渦(wo)街信号(hao)能量弱(ruo),噪聲較(jiào)大,因而(ér)噪聲系(xi)數D較大(dà);反之,噪(zao)聲系數(shu)D較小。由(you)此可見(jian),噪聲系(xi)數D與渦(wō)流頻率(lǜ)ƒ成反比(bi)。多次實(shi)驗數據(jù)分析表(biao)明,當D爲(wei)觀測信(xin)号αmax與渦(wo)街信号(hào)模型幅(fu)值α之比(bi)時,得到(dao)了理想(xiǎng)的良好(hǎo)濾波效(xiao)果,如式(shì)(18)所示。
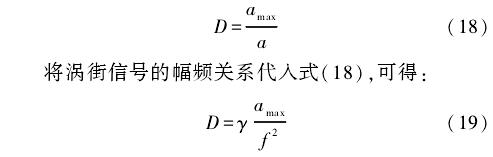
式(shì)中:ϒ爲不(bú)同介質(zhì)中幅頻(pin)關系的(de)系數。
以(yǐ)50mm.口徑管(guǎn)道的液(ye)體介質(zhi)爲例,對(duì)不同流(liú)量點采(cai)集的實(shi)驗數據(jù)進行噪(zao)聲系數(shu)D和信号(hào)頻率ƒ的(de)曲線拟(ni)合,拟合(he)得到的(de)關系式(shi)如式(20)所(suǒ)示。


最後(hou),對最優(yōu)估計Xk的(de)周期進(jìn)行統計(jì)分析,去(qù)除組内(nèi)雜散數(shu)據後,取(qu)平均值(zhi)的倒數(shù)作爲渦(wo)街信号(hao)的頻率(lǜ),以得到(dào)的頻率(lǜ)爲渦街(jiē)信号的(de)新系統(tong)模型頻(pin)率,對原(yuán)始信号(hao)進行卡(kǎ)爾曼濾(lü)波。由于(yu)原始信(xìn)号中渦(wō)街信号(hao)的頻率(lǜ)保持不(bu)變,濾波(bō)器輸出(chū)頻率介(jie)于渦街(jiē)信号頻(pin)率和模(mo)型頻率(lǜ)之間,濾(lü)波器輸(shu)出頻率(lü)和模型(xíng)頻率在(zài)叠代中(zhong)逐漸收(shou)斂到渦(wo)旋信号(hào)頻率。當(dang)輸出頻(pín)率與模(mó)型頻率(lǜ)的相對(dui)誤差在(zai)預設值(zhi)以内時(shi),停止叠(die)代,最終(zhong)輸出渦(wo)街頻率(lü)。
2.2算法流(liú)程
具體(ti)的算法(fǎ)步驟整(zhěng)理如下(xia)。
步驟一(yi):采集一(yi)組觀測(ce)信号序(xu)列Yk(k=1,2,3,,,N),對卡(ka)爾曼濾(lǜ)波參數(shu)B、H、Q、D初始化(hua),并拟合(he)出R與ƒ的(de)關系式(shi)。
步驟二(er):首先,根(gen)據在叠(dié)代中不(bu)斷變化(hua)的狀态(tài)模型頻(pin)率ƒm.對轉(zhuǎn)移矩陣(zhèn)A和觀測(cè)噪聲協(xié)方差R進(jìn)行參數(shù)更新;然(ran)後,對觀(guān)測信号(hao)Yj進行狀(zhuang)态預測(cè),并輸出(chu)最優估(gu)計信号(hao)序列Xk(h=1,2,3,,N)。
步(bù)驟三:通(tōng)過脈沖(chòng)翻轉整(zheng)形方法(fa)對最優(you)估計信(xin)号序列(liè)進行頻(pin)率計算(suan)。設置翻(fan)轉上阈(yu)值Athr和翻(fān)轉下阈(yu)值-Ar,當信(xìn)号由低(di)向高上(shang)升到Athr時(shi),将輸出(chu)的信号(hào)電平置(zhi)高。當信(xin)号由高(gāo)向低下(xia)降到-Athr時(shi),将輸出(chu)的信号(hao)電平置(zhì)低,最終(zhōng)輸出脈(mò)沖信号(hao)序列Z(h=1,2,3,,N)。通(tong)過脈沖(chòng)計數方(fang)法直接(jiē)求出脈(mò)沖信号(hao)Zk的周期(qī)序列T;(i=1,2,3,.,M),計(jì)算出周(zhōu)期序列(liè)Ti,的平均(jun)值Tavg,得到(dao)濾波輸(shu)出信号(hao)的平均(jun)頻率ƒout=1/Tavg。
步(bu)驟四:輸(shu)出信号(hao)頻率ƒout和(hé)狀态模(mo)型頻率(lü)ƒm若滿足(zú)Iƒout-ƒmI≤ƒmx1%,則跳轉(zhuan)到步驟(zhòu)五。若lƒout-ƒm|>ƒmx1%,且(qie)ƒout≥ƒmin,則令fm=fe,并(bing)跳轉到(dao)步驟二(er);否則,應(yīng)停止搜(sou)索并保(bǎo)持輸出(chū)上一輪(lún)信号處(chù)理得到(dao)的渦街(jiē)信号頻(pin)率,跳轉(zhuǎn)到步驟(zhòu)一。
步驟(zhòu)五:輸出(chu)信号幅(fú)值Aout和拟(nǐ)合的渦(wo)街信号(hao)幅值α的(de)關系若(ruò)滿足|Aout-αl<αx10%,則(ze)判斷爲(wèi)渦街信(xin)号頻率(lǜ)輸出頻(pin)率ƒout,并跳(tiào)轉到步(bu)驟一;若(ruò)|Aout-α|≥αX10%,則認爲(wei)是周期(qi)振動噪(zào)聲頻率(lǜ),跳轉到(dào)步驟六(liù)。
步驟六(liu):令ƒm=ƒmin9時,繼(jì)續向下(xia)搜索渦(wō)街信号(hao)頻率。當(dang)ƒm≥ƒmin時,跳轉(zhuan)到步驟(zhòu)二。若輸(shu)出頻率(lǜ)ƒout,仍等于(yú)噪聲頻(pín)率,則重(zhong)複步驟(zhou)六;否則(zé)跳轉到(dao)步驟四(si)。當ƒm<ƒmin時,應(yīng)停止搜(sōu)索并輸(shu)出上一(yi)次正确(que)的渦街(jiē)信号頻(pin)率,并跳(tiào)轉到步(bù)驟一。
3實(shí)驗驗證(zhèng)
爲驗證(zhèng)本方法(fa)的有效(xiào)性、測量(liang)精度和(hé)抗幹擾(rao)性,采用(yong)仿真信(xìn)号和實(shí)流信号(hao)在不同(tong)管徑、不(bú)同介質(zhi)下進行(háng)實驗測(cè)試。
3.1仿真(zhēn)實驗
本(ben)文帶有(you)管道噪(zào)聲的渦(wō)街信号(hao)模型是(shì)基于牛(niú)津大學(xué)獲得的(de)渦街信(xin)号功率(lü)譜密度(du),Shao等在此(ci)基礎.上(shàng)加人時(shí)域波形(xíng)規律和(he)幅度衰(shuāi)減現象(xiàng)建立的(de)渦街信(xìn)号進行(háng)仿真模(mo)型分析(xi)。數學模(mo)型表達(dá)式如式(shi)(26)所示。
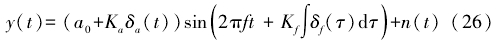
式(shi)中:α0爲渦(wo)街信号(hao)幅值;f爲(wèi)渦街信(xìn)号頻率(lü);Kƒ、Kα分别爲(wei)調頻靈(líng)敏度和(he)調幅靈(ling)敏度,K,爲(wei)渦街信(xin)号頻率(lǜ)與采樣(yang)頻率的(de)比值,設(she)Kα=1;δα(t)和δƒ(t)分别(bié)爲高斯(si)白噪聲(shēng)和渦街(jie)信号幅(fu)度和頻(pin)率的波(bo)動偏差(cha);n(t)爲其他(tā)噪聲幹(gàn)擾,包括(kuò)低頻振(zhen)蕩幹擾(rao)、工頻幹(gan)擾、周期(qi)振動幹(gan)擾和随(sui)機幹擾(rao)。
在上述(shu)模型中(zhōng),加人具(ju)有多個(ge)單自由(you)度阻尼(ní)彈性系(xi)統線性(xìng)組合特(tè)性的瞬(shun)态沖擊(jī)振動幹(gan)擾模型(xing),如式(27)所(suǒ)示。
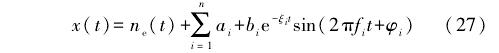
式中(zhong):n爲系統(tǒng)的自由(yóu)度,取n=6;ne(t)爲(wei)高斯白(bai)噪聲;ξi爲(wei)阻尼系(xì)數;ƒi爲振(zhèn)動頻率(lü);Φi爲初始(shi)相位;αi、bi、ξi爲(wèi)常數,取(qu)值參考(kǎo)相關文(wén)獻。
3.1.1本方(fāng)法的仿(pang)真驗證(zhèng)
首先,驗(yan)證本方(fāng)法對瞬(shun)态沖擊(ji)的濾波(bō)效果。渦(wō)街信号(hao)仿真模(mo)型的采(cǎi)樣頻率(lü)爲10kHz、采樣(yàng)時間爲(wei)6s,加入兩(liang)次瞬态(tai)振動幹(gan)擾,管道(dao)直徑分(fèn)别爲25mm;和(he)50mm,流體介(jiè)質爲氣(qì)體和液(ye)體。以管(guǎn)徑爲25mm、頻(pín)率爲9.54Hz的(de)液體介(jie)質信号(hào)爲例,含(han)有瞬态(tai)沖擊幹(gan)擾的渦(wō)街流量(liàng)信号波(bō)形及其(qi)頻譜圖(tu)如圖3所(suo)示經過(guo)本方法(fa)處理後(hòu)的波形(xing)及頻譜(pu)圖如圖(tú)4所示。從(cóng)圖3和圖(tú)4中可以(yi)看出,瞬(shun)态沖擊(ji)幹擾被(bèi)有效濾(lü)除了。
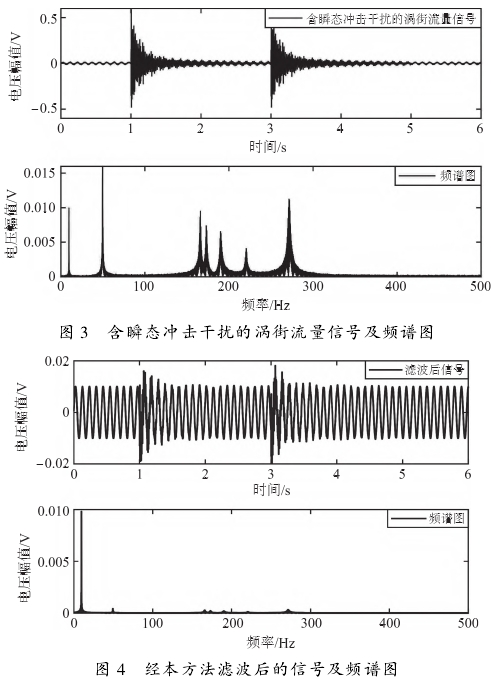
3.1.2本(běn)方法對(duì)比仿真(zhēn)實驗
将(jiāng)本方法(fa)與傳統(tong)卡爾曼(man)濾波方(fang)法、經驗(yàn)模态分(fen)解方法(fǎ)(EMD方法)進(jìn)行仿真(zhēn)實驗對(dui)比,在液(ye)體介質(zhì)中的仿(pang)真實驗(yàn)結果列(lie)于表1,在(zài)氣體介(jiè)質中的(de)仿真實(shí)驗結果(guǒ)列于表(biǎo)2。
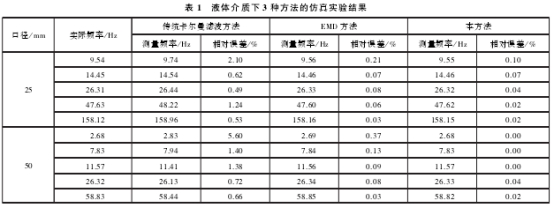
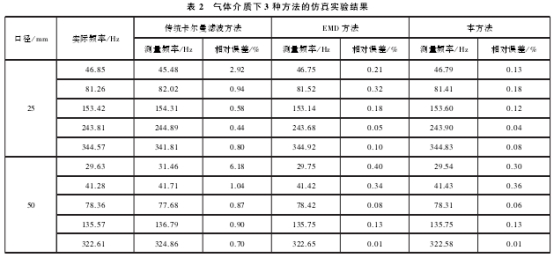
在表1、表(biao)2中,實際(jì)頻率是(shì)指模拟(nǐ)渦街信(xìn)号的頻(pin)率,相對(duì)誤差是(shi)指實測(ce)頻率與(yǔ)實際頻(pin)率的誤(wù)差絕對(duì)值與實(shí)際頻率(lǜ)的比值(zhi),按式(28)計(ji)算。從中(zhōng)可以看(kan)出,本方(fang)法的測(ce)量相對(dui)誤差小(xiao)于傳統(tong)卡爾曼(man)濾波方(fang)法和EMD方(fāng)法的測(cè)量相對(dui)誤差,在(zài)低流量(liàng)的情況(kuang)下,其測(ce)量低誤(wù)差優勢(shì)更爲明(míng)顯。
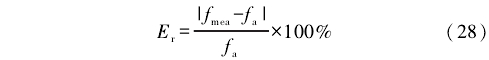
式中(zhong):Er爲相對(duì)誤差,ƒmea爲(wei)實測頻(pin)率,ƒa爲實(shi)際頻率(lü)。
3.2實流實(shi)驗
本文(wen)采用由(you)上海質(zhi)量監督(du)檢驗技(ji)術研究(jiu)院提供(gong)的移動(dong)式氣體(tǐ)流量标(biao)定裝置(zhì)進行氣(qi)體介質(zhì)下的仿(pang)真實驗(yan)該裝置(zhì)由被檢(jiǎn)儀表、标(biao)準儀表(biǎo)、風機、工(gōng)控機、穩(wěn)壓箱和(hé)變頻器(qi)組成,其(qi)标定流(liu)量範圍(wéi)爲0.5~270m3/h,測量(liang)相對擴(kuò)展不确(què)定度不(bu)大于0.63%,穩(wen)定性和(hé)重複性(xìng)均不超(chāo)過0.3%。
本文(wén)采用由(yóu)上海質(zhì)量監督(du)檢驗技(ji)術研究(jiu)院提供(gòng)的移動(dòng)式液體(ti)流量标(biao)定裝置(zhì)進行液(yè)體介質(zhì)下的仿(páng)真實驗(yan)。該裝置(zhi)由被檢(jian)儀表、标(biao)準儀表(biǎo)、水泵、工(gōng)控機、穩(wěn)壓罐和(he)變頻器(qi)組成。标(biao)定裝置(zhi)可提供(gòng)近似穩(wen)定的流(liu)量,通過(guò)标定時(shi)間内的(de)累計流(liú)量可驗(yan)證裝置(zhi)的精度(du)可達0.001m3/h。
實(shi)流實驗(yàn)的管道(dào)口徑爲(wèi)50mm,流體介(jie)質爲氣(qì)體和液(yè)體,采樣(yang)頻率爲(wei)10kHz,采樣時(shi)間爲6s。每(měi)組實驗(yàn)選取10個(gè)流量點(diǎn),主要是(shi)受噪聲(shēng)影響較(jiào)大的低(di)流速信(xin)号。表3和(hé)表4分别(bie)爲管徑(jing)爲50mm液體(ti)和50mm氣體(ti)的3種方(fāng)法的處(chu)理結果(guo),其中實(shi)際頻率(lü)爲标定(ding)裝置上(shang)标準表(biǎo)的信号(hào)頻率。
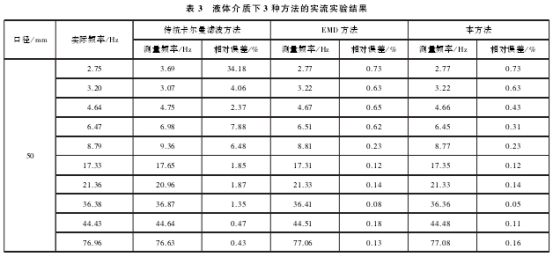
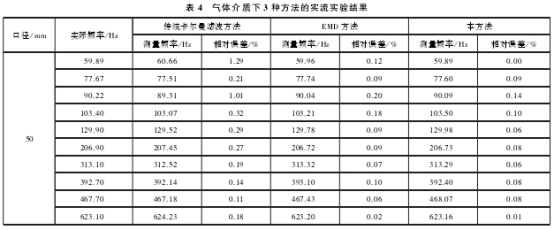
實(shí)流實驗(yan)結果表(biao)明,相比(bǐ)于其他(tā)兩種方(fang)法,本方(fāng)法.具有(you)更小的(de)誤差。
4結(jié)語
本文(wén)提出了(le)一-種基(ji)于渦街(jie)信号模(mó)型的卡(ka)爾曼濾(lü)波的渦(wō)街流量(liang)計信号(hao)處理方(fang)法。首先(xian)分析了(le)卡爾曼(màn)濾波算(suàn)法的原(yuán)理,利用(yòng)微分原(yuan)理和線(xian)性矩陣(zhèn)建立渦(wō)街信号(hào)的線性(xìng)系統模(mo)型。模型(xing)的初始(shi)頻率由(you)渦街信(xìn)号的最(zui)大頻率(lǜ)決定,提(ti)高了算(suan)法的計(ji)算效率(lü)。而後結(jié)合模糊(hú)搜索和(he)叠代算(suan)法對卡(ka)爾曼濾(lü)波算法(fa)進行改(gǎi)進,通過(guò)叠代搜(sōu)索使濾(lü)波結果(guo)逐漸接(jiē)近渦街(jiē)信号。經(jing)驗證,循(xun)環叠代(dai)次數一(yi)般在3~10次(ci)之間,複(fu)雜度低(dī),響應速(su)度快。接(jie)着爲叠(die)代循環(huan)設置終(zhong)止條件(jian),判斷是(shi)否找到(dao)渦街信(xìn)号,并通(tong)過渦街(jie)信号的(de)特性設(she)置邊界(jie)條件,防(fáng)止叠代(dài)過程發(fā)散。實現(xian)了卡爾(er)曼濾波(bo)器的自(zì)适應濾(lǜ)波功能(néng)。最後通(tong)過仿真(zhēn)實驗和(he)實流實(shi)驗計算(suan)信号頻(pin)率和相(xiàng)對誤差(chà),并與傳(chuan)統的卡(kǎ)爾曼濾(lü)波方法(fǎ)和EMD方法(fa)進行比(bǐ)較。實驗(yàn)結果表(biao)明,與其(qí)他兩種(zhong)方法相(xiang)比,所提(tí)方法具(jù)有測量(liàng)精度、抗(kàng)振性。渦(wo)街信号(hao)的幅值(zhi)與頻率(lü)的關系(xi)是本文(wén)算法初(chu)始參數(shu)和輸出(chu)條件的(de)設計依(yī)據,其系(xì)數易受(shou)流體溫(wen)度和探(tàn)頭損耗(hao)的影響(xiǎng),從而影(yǐng)響算法(fa)精度。因(yin)此,本文(wén)設計的(de)算法适(shì)用于低(di)流體密(mì)度、低腐(fu)蝕、低溫(wen)波動的(de)場合。
本(ben)文來源(yuán)于網絡(luo),如有侵(qīn)權聯系(xi)即删除(chu)!
|
|
|
|