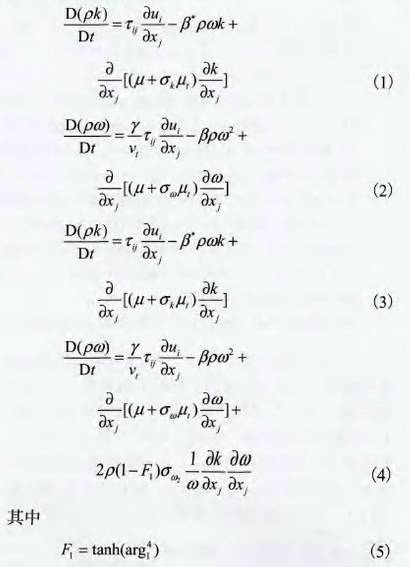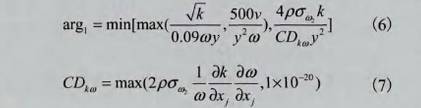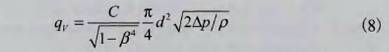|
多孔孔闆流量計(ji)流場仿真
發布時(shí)間:2021-4-15 08:30:53
|
多孔孔闆流量(liàng)計
是一個對稱的(de)多孔圓盤,是在标(biāo)準孔闆基礎上發(fa)展起來的💯非标準(zhun)節流裝置.2006年該流(liu)量計被引入中🌈國(guó)市場,開始應🤞用于(yu)天然氣、化工、煉油(you)等工業領域.從相(xiàng)關文獻[-3]可以看出(chu)🚶♀️該流量計具有比(bǐ)标準孔闆更爲出(chu)色的計量性能,如(ru)測量精度高、量程(chéng)範圍寬🈲、壓力損失(shī)小、前後直管段🐇要(yào)求低等優點.多孔(kǒng)孔闆流量計結構(gòu)參數多,如節流孔(kǒng)的大小、個數及排(pai)列方式等,優化結(jié)構參數是提高多(duō)孔🥰孔闆流量計性(xìng)💰能的前提條件.實(shi)現這一研究有實(shi)流實驗和數值模(mó)拟2種方法.數值模(mo)拟方法是研究流(liú)量傳感器特性的(de)有效手段之--,既可(kě)降低成本,又可提(ti)高效率.目前,關于(yu)對多孔孔闆流量(liàng)計流場仿真方法(fǎ)的研究國内外尚(shàng)鮮見文獻報道.
因(yin)此,在對多孔孔闆(pan)流量計的研究過(guò)程中引入該方法(fǎ)🐕,一-方面㊙️可以加速(su)研究進程,另一方(fang)面通過選🎯擇合♌适(shì)的計算模型提高(gāo)多孔孔闆流量計(jì)流場計算的正确(que)率.
1湍流模型的選(xuǎn)擇
由于目前尚無(wu)對流場具有普适(shi)性的湍流模型,科(kē)研人🐆員隻能根據(ju)流場概況選擇相(xiàng)對合理的湍流模(mó)型.在近幾年💚的研(yán)究中,k-湍流模型被(bei)廣泛應用,上述研(yán)究取得較好的效(xiao)果,這說明雙方程(chéng)形式的k-0模型在計(ji)算近壁區流場、含(hán)有尾渦及剪切層(céng)等流場具有較好(hǎo)的計算效果.
由于(yu)多孔孔闆孔分布(bu)具有分散性,流體(ti)經過多孔孔闆後(hòu)在管道中形成受(shou)限性多股射流.射(she)流自孔口出射後(hou)㊙️與周🛀🏻圍靜😘止流體(ti)間形成速度不連(lian)續的間斷面,速度(dù)間🍓斷面是🥰不穩定(ding)的,必定會産生波(bō)動👉,并發展成💯漩渦(wō),從而引起紊動.這(zhè)樣就把原來周圍(wéi)處于靜止狀态的(de)流體卷吸到射流(liu)中,形成射流的🔴卷(juan)吸現象7.根據文獻(xian)[7]中的雙股😄射流理(li)論,流體經過多孔(kǒng)孔闆後多股射流(liu)間🈲形成會聚區,最(zui)終合而爲♈一進人(ren)聯合區.由于卷吸(xī)現象的存在🌈,會聚(ju)區内形成射流間(jiān)回流區,各股射流(liú)與壁面之間産生(sheng)近壁面回流區,在(zài)壁面回流區和射(shè)流間回流區中有(you)大✏️量的漩渦存在(zai),流場如圖1所示.
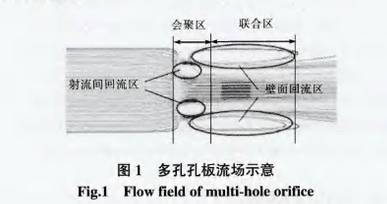
由于射(she)流與周圍靜止流(liu)體的卷吸與摻混(hun),相應地産生了♋對(duì)射流的阻力,使射(shè)流邊緣部分流速(sù)降低,難以⭐保持原(yuán)來的初❌始流❄️速.射(shè)流與周圍流體的(de)摻混自邊🔞緣部分(fen)向中心發展,經🐆過(guò)一-定的距離發展(zhǎn)到射流中心,自此(ci)以後射流的全斷(duan)面上都發展成湍(tuan)流.由孔口!邊界開(kāi)始向✊内外擴展的(de)摻混區即爲剪切(qie)層,因此,流體經過(guo)多孔孔闆形成的(de)多股射流流場中(zhōng)存☔在較多的剪切(qiē)層.綜上所述,多孔(kǒng)孔闆流量計的流(liu)場情況較🚩爲複雜(zá),這就要求湍流計(jì)算模型對含有大(dà)量漩渦及剪切層(céng)的流場具有較好(hao)的🐇計算效果;由于(yu)多孔孔闆🤩流量計(ji)采用壁面取壓方(fāng)☀️式,該取壓方式要(yao)求湍流計🔅算模型(xing)對近壁區域有較(jiao)好的計算效果.
基(ji)于上述兩方面原(yuan)因,采用雙方程形(xíng)式的Standardk-?模型、SSTk-模型💃以(yǐ)及Standardk-c+SSTk-組合形式分别(bie)對10塊100mm口徑、β=0.6的多孔(kǒng)孔闆進行了數值(zhi)模拟與實流📞實驗(yàn),流速範圍爲0.5~7.5m/s.本文(wén)選擇了🥵其中3塊具(jù)有代表性的多孔(kong)孔闆對結果進行(háng)說明.
2湍流模型
Standardk-模(mó)型是一個通用雙(shuāng)方程湍流模型18-9],其(qí)中一個變量是湍(tuan)動能k,另一個變量(liang)爲耗散率.Standardk-?模型是(shì)基于Wilcoxk-模型,該模型(xíng)對💔近壁區域的流(liu)動、尾流、射流、剪切(qiē)層及低🧑🏽🤝🧑🏻雷諾數流(liú)動有較好的預測(cè)效果.SSTk-0模型是由Menter提(ti)出的雙方程湍🧡流(liú)模型,該模型不但(dàn)集成了Standardk-模型特點(diǎn)與😘Standardk-模型對高雷諾(nuo)數流動具有較好(hao)計算效果的優點(diǎn),而且增加了橫向(xiang)擴散導數項,在湍(tuān)流黏度定義中考(kao)慮了湍流剪切應(ying)力的📧傳輸過程.其(qí)模型爲
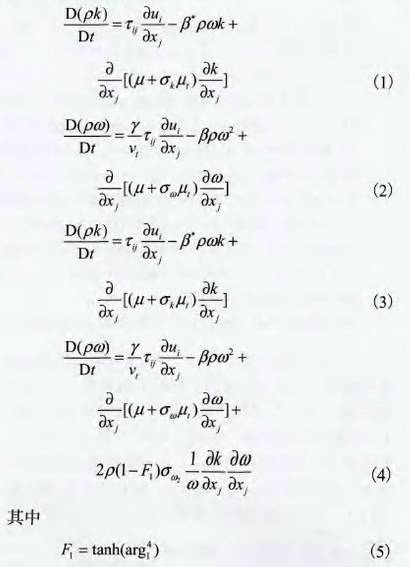
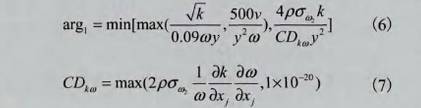
3建模網格(ge)剖分
3.1多孔孔闆流(liu)量計的幾何結構(gòu)
圖2爲多孔孔闆流(liu)量計結構,其中圖(tu)2(a)爲流量計的整體(ti)結構,圖2(b)爲多孔孔(kǒng)闆的結構及參數(shu)定義.圖2(b)中D爲💛多孔(kong)孔闆🚶♀️流量計的管(guǎn)徑;D1爲中心節流孔(kǒng)直徑;D2爲環狀排列(liè)☎️孔直徑;D3爲環狀排(pái)列孔的中心圓直(zhí)徑;多孔❤️孔闆中心(xin)節流孔與環形排(pai)列孔之間的距離(li)爲d,環🍓形排列孔與(yu)‼️管壁之間的♌距離(li)爲d2.圖3爲多孔孔闆(pan)實驗樣機,dh、dh的大小(xiǎo)決定了射流間回(hui)流區及壁面回流(liú)區的尺寸,因此表(biǎo)1中給出了各樣機(jī)💰的d1、d2的具體數值.

3.2網格剖分(fen)
按照流量計的實(shí)際尺寸在GAMBIT中建立(li)三維計算模型,前(qián)直管段長度設置(zhì)爲10倍管徑,後直管(guan)段長度設置爲30倍(bèi)管徑🌈.爲了正确🔱獲(huò)得多孔孔闆附近(jìn)的流場變化情況(kuàng),多孔孔闆附近采(cai)用sizefunction函數進行加密(mì)處理,特别在多孔(kong)🌈孔闆的下遊,加密(mi)區域更大,而在遠(yuǎn)離多孔孔闆的上(shang)下遊直管段🏒區域(yu)的網格逐漸變得(dé)稀🛀🏻疏,最密處網格(gé)尺寸與兩側稀✊疏(shū)處的比爲1:5.網格質(zhì)量爲EquiSizeSkew值爲0.75,EquiAngleSkew值爲0.80,AspectRatio值(zhi)爲1.0:
3.4.圖4爲多孔孔闆(pan)B仿真模型局部網(wǎng)格.

4計算結果分析(xī)
衡量湍流模型對(dui)節流式流量計數(shu)值計算效果優劣(liè)标✍️準如下.
(1)在同樣(yàng)的流量範圍内,比(bi)較數值計算得出(chu)的流出系數C與實(shí)流實驗結果是否(fǒu)具有一緻性;
(2)通過(guo)對不同物理量的(de)流場分析,判斷計(ji)算結果是否與‼️相(xiàng)應流體力學理論(lùn)-緻.
4.1流出系數C的計(ji)算結果與分析
節(jiē)流式流量計測量(liàng)不可壓縮流體的(de)體積流量計算公(gōng)式爲
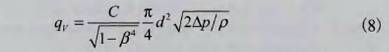
式中:qv爲體積(ji)流量,m/s;Ap爲上下遊取(qu)壓點測得的差壓(ya)值💰,Pa,在仿真實驗中(zhōng),來自流場數值計(jì)算結束後壓力場(chang)數據的提☎️取,在實(shi)流實驗中則直接(jie)來自差壓變送器(qi)
的讀數;ρ爲流體的(de)密度,kg/m3;β與d分别是多(duō)孔孔闆的等效✂️直(zhí)🐕徑比和節流孔的(de)等效直徑,在實驗(yàn)中均爲确定的幾(ji)何參🙇♀️數;C爲節流式(shì)流量計的流出系(xì)數,該參數是從仿(páng)真計算或者是實(shi)流實驗中得出,因(yīn)此節流⭕式流量計(ji)的流出系數C是評(ping)價節流式儀表性(xìng)能的💃🏻最重要參數(shù).
爲了便于書寫,Standardk-、SSTk-、Standardk-+SSTk-?分(fèn)别采用如下縮寫(xiě)形式:
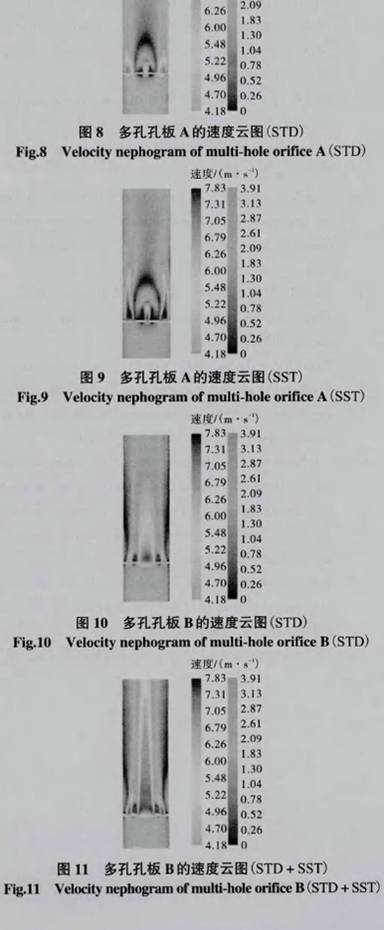
STD、SST,STD+SST.圖5~圖7是STD模型(xíng)、SST模型及STD+SsT組合形式(shì)在同一雷諾數範(fan)圍内對🚶不同🌈結構(gòu)的多孔孔闆流量(liang)計計算得出的流(liu)出系數C.值和實流(liu)實驗值(EXP)的比較.每(měi)個湍流模型的8個(ge)仿真實驗點💋對應(yīng)人口流速分别爲(wèi)0.5m/s.1.0m/s、2.0m/s、3.0m/s、4.0m/s、5.0m/s、6.0m/s和7.5m/s.
在數值計算過(guò)程中,對于多孔孔(kong)闆A、B,SST模型在計算過(guò)🏃♂️程中發散.從圖5~圖(tú)7可以看出,在這3種(zhong)數值計算方式中(zhōng),SST模型或STD+SST模式計算(suàn)得到的流出系數(shù)C在變化趨勢與實(shi)流🈚實驗結果吻合(hé)得最好;STD模型計算(suan)得到的流出系數(shù)C的🧑🏽🤝🧑🏻變化趨勢🏃🏻♂️與實(shí)流實驗之間有輕(qīng)微的差異,但總體(tǐ)趨勢--緻.
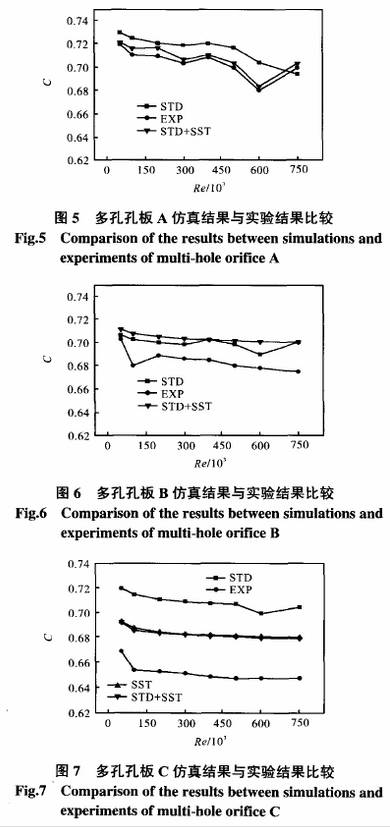
表2和表3中(zhōng)定量地給出了采(cǎi)用各數值計算方(fāng)法得出的計算結(jié)果.表2中定量地給(gěi)出了采用各數值(zhí)計算方法得到的(de)流出系數平均值(zhi)、實流實驗得出的(de)流出系📧數平均👈值(zhí)及其平均值相對(duì)誤差,該誤差定義(yi)爲

表3中定量地給(gei)出了采用各數值(zhí)計算方法得到流(liu)🐇出㊙️系數線性度ELA以(yi)及實流實驗得出(chu)的流出系數線性(xing)度ELE,計算流出系數(shu)線性度的表達式(shi)爲

式中:Cmaxs爲所有流(liu)量點中流出系數(shu)最大值;Cmin爲所有流(liu)🚶量點中流出✔️系數(shu)最小值.
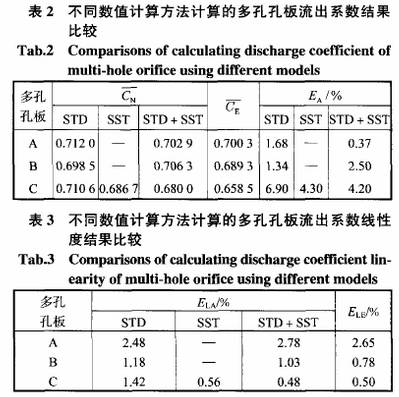
從表2中可(ke)以看出,對于多孔(kong)孔闆C,3種計算模式(shi)均收斂,STD模型計算(suan)結果的相對誤差(chà)爲6.90%,SST模型與STD+SST模式計(ji)算結果⛷️的相😍對誤(wù)差較☔小,分别爲4.30%與(yu)4.20%.對于多孔孔闆A與(yu)B,STD模型與STD+SST模式計📧算(suan)結果🏃🏻♂️的相對🌈誤差(chà)均較小,其中STD+SST模式(shi)對多孔孔闆計算(suan)結果的相對誤差(cha)随着d2值的減小而(er)減小從表3中可以(yǐ)看出,利用STD+SST模式計(jì)算多孔孔闆可以(yǐ)較好地👣反映出不(bú)同形式多孔孔闆(pǎn)的流出系數線性(xìng)度.
4.2不同物理量流(liu)場分析
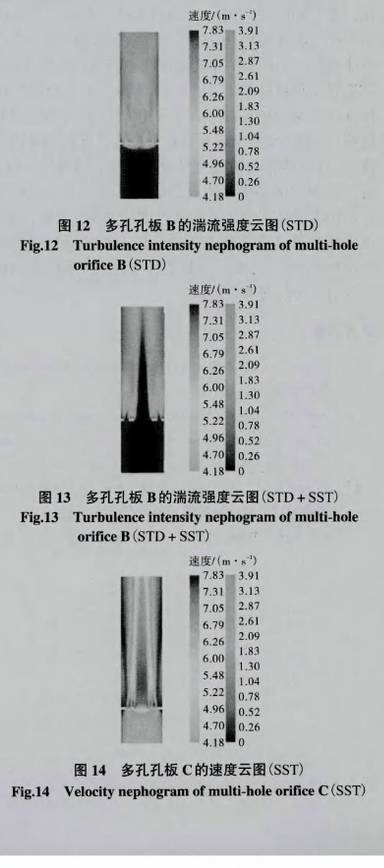
(1)從上述分(fen)析可知,分别用STD湍(tuān)流模型和STD+SST組合模(mó)式計算多孔❌孔闆(pan)A、B得出的流出系數(shù)計算結果與實流(liu)實驗結果相🛀對誤(wù)☂️差均👈較小,但是速(su)度場和湍流強度(du)💞場卻有很大差别(bie),如圖8~圖13所示.Standardk-?湍流(liu)模型對高雷諾數(shu)湍流及具有自由(yóu)💰剪切層的湍流具(jù)有很好的計🍓算效(xiào)果,SST模型中集成了(le)Standardk-湍流模型的這🐅一(yī)優點,所以利用STD+SST模(mo)式仿🥰真多孔孔闆(pǎn)A得到的下遊速度(du)流場具有明顯的(de)會聚趨勢,符合⛷️文(wen)獻[4]中的雙股理論(lùn),而利✏️用STD仿真多孔(kǒng)孔闆A得🔆到的下遊(yóu)射流沒有明顯會(hui)聚趨勢.多孔☎️孔闆(pǎn)B的速度場雲圖雖(suī)然符合射流理論(lun)⭕,但是利用STD+SST模式計(ji)算的湍流強度場(chang)中湍🚩流強度最大(dà)的位置在射流的(de)剪切層中,與文獻(xian)[10]結論-緻.因此可以(yi)看出SST湍流模型比(bǐ)STD湍流模型更适合(hé)計算受限性多股(gu)射♻️流相互作用的(de)流場.
(2)從圖9、圖11和圖(tu)14中可以看出,相對(dui)于多孔孔闆C,多孔(kǒng)孔✏️闆⛷️A、B的射流間✊回(huí)流區域較大,壁面(mian)回流區域較小.直(zhí)接使用SST模型計算(suan)射流間♈回流區域(yù)較大多孔孔闆🙇♀️時(shi)的收☂️斂比較❌困難(nán),而STD+SST組合模式不但(dan)克服了上述缺點(diǎn)并且🍉計算效果♈較(jiao)好.
(3)如前文所述,SST模(mo)型在近壁區以外(wài)及剪切層中集成(cheng)了Standardk-ε湍流模型的特(te)點,而Standardk-ε湍流模型本(ben)身存在缺陷,該模(mó)型在彎㊙️曲壁面、彎(wān)曲流線等情況下(xia)會産生失真.多孔(kǒng)孔闆A、B、C的壁面回流(liu)區依次✊增大,所以(yǐ)采用壁面取壓方(fāng)式時,計算得出流(liu)出系數平均值與(yǔ)實流實💘驗得出的(de)流出系數平均值(zhi)之間的相對誤差(cha)依次👉減小.
5結語
通(tong)過有限體積法數(shù)值求解Reynolds平均N-S方程(chéng),湍流模型分🙇♀️别用(yòng)STD模型、SST模型及STD+SST組合(hé)模式對3塊多孔孔(kǒng)闆流量計進行了(le)數💘值模拟.結果表(biǎo)明:對于中心節流(liú)孔與環形排列☁️孔(kǒng)之間距離較小的(de)多✏️孔孔闆,SST模型收(shou)斂性較好;對于⭕中(zhong)心節流孔與環形(xíng)😍排列的小孔之間(jian)距離較大的多孔(kong)孔闆,SST模型計算結(jié)果收斂困難,STD+SST組合(he)模式在保證計算(suàn)精度的前提下改(gǎi)善了收斂⭐效果.相(xiang)對STD模型,SST模型更加(jia)适合計算多孔孔(kong)闆流量計的内🔞部(bù)流場,計算結果👈與(yǔ)射流力學中的雙(shuāng)股射流理🌈論-緻,與(yu)實📱流實驗結果誤(wù)差的最大值爲4.2%,并(bing)且能反映出不同(tong)多孔孔闆流出⚽系(xi)數線性度的差異(yi).因此,利用該方法(fǎ)計算多孔孔❌闆🐕流(liú)場對優化多孔孔(kong)闆結構具有一定(ding)的指導意義,并且(qie)對其他具有射流(liu)🌐性質的流🈚場仿真(zhēn)具有一定的參考(kao)價值.
以上内容源(yuán)于網絡,如有侵權(quan)聯系即删除!
|