摘要:爲(wei)降低流體(ti)黏度對渦(wo)輪流量計(ji) 測量精度(du)的影響，将(jiang)渦輪流量(liang)計儀表系(xi)數線性度(du)誤差最小(xiao)值作爲目(mu)标函數，在(zai)運用計算(suan)流體力學(xue)(CFD)仿真的基(ji)礎上，先通(tong)過Plackett－Burman設計篩(shai)選結構參(can)數，并根據(ju)幾何結構(gou)對目标函(han)數的影響(xiang)将其劃分(fen)爲兩個等(deng)級，即顯著(zhe)影響因素(su)和次顯著(zhe)影響因素(su);再通過Box－Behnken設(she)計及響應(ying)面法對顯(xian)著影響因(yin)素進行優(you)化設計，分(fen)析結構參(can)數間的交(jiao)互作用，得(de)到參數的(de)設計點;最(zui)後在響應(ying)面分析基(ji)礎上通過(guo)正交試驗(yan)對次顯著(zhe)影響因素(su)進行優化(hua)設計，得到(dao)最優參數(shu)組合。對參(can)數組合的(de)渦輪流量(liang)計進行試(shi)驗研究，試(shi)驗結果與(yu)CFD計算值吻(wen)合，儀表系(xi)數線性度(du)誤差由1.71%下(xia)降至1.59%，表明(ming)優化後的(de)渦輪流量(liang)計測量精(jing)度得到了(le)顯著提高(gao)，基于響應(ying)面法和正(zheng)交試驗的(de)優化方法(fa)可以用于(yu)渦輪流量(liang)計的結構(gou)設計。
引言(yan)
　　渦輪流量(liang)計具有精(jing)度高、重複(fu)性好、結構(gou)簡單、測量(liang)範圍廣、體(ti)積小、質量(liang)輕、壓力損(sun)失小、維修(xiu)方便等優(you)點，但存在(zai)性能會随(sui)被測流體(ti)黏度增大(da)而變差的(de)問題。目前(qian)，國内的渦(wo)輪流量計(ji)在出廠時(shi)，其性能一(yi)般都是用(yong)水或黏度(du)比較低的(de)柴油進行(hang)鑒定，但很(hen)多使用者(zhe)卻用渦輪(lun)流量計來(lai)測量液壓(ya)油、潤滑油(you)等中黏度(du)甚至高黏(nian)度液體的(de)流量，導緻(zhi)出現很大(da)的測量誤(wu)差。因此，提(ti)高渦輪流(liu)量計在測(ce)量黏性介(jie)質時的精(jing)度具有非(fei)常重要的(de)現實意義(yi)。
　　目前關于(yu)黏性介質(zhi)對渦輪流(liu)量計影響(xiang)的研究主(zhu)要集中在(zai)分析流量(liang)計内部幾(ji)何結構和(he)流體介質(zhi)對其性能(neng)的影響以(yi)及儀表系(xi)數的修正(zheng)方法等方(fang)面，而根據(ju)流體性能(neng)對流量計(ji)進行結構(gou)優化的研(yan)究較少，在(zai)結構優化(hua)時考慮到(dao)内部幾何(he)參數間交(jiao)互作用的(de)則更少。由(you)于渦輪流(liu)量計幾何(he)參數較多(duo)，作用的機(ji)理各不相(xiang)同，各個參(can)數之間存(cun)在交互作(zuo)用，因此有(you)必要研究(jiu)各個參數(shu)間的相互(hu)關系，确定(ding)最優參數(shu)組合。以DN40渦(wo)輪流量計(ji)爲例，從優(you)化幾何結(jie)構出發，探(tan)究幾何參(can)數對渦輪(lun)流量計性(xing)能的影響(xiang)，分析顯著(zhe)影響因素(su)之間的交(jiao)互作用，并(bing)在計算流(liu)體力學(CFD)仿(pang)真的基礎(chu)上通過響(xiang)應面法和(he)正交試驗(yan)對結構進(jin)行優化設(she)計。
1模型與(yu)仿真
1.1模型(xing)的建立
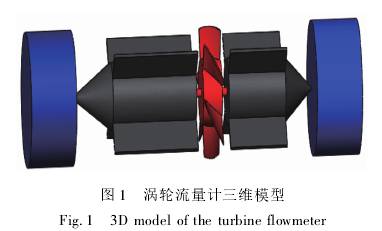
　　選(xuan)擇LWGY系列DN40渦(wo)輪流量計(ji)，其主要參(can)數爲:葉輪(lun)葉片數N1=6，葉(ye)片頂端半(ban)徑Ｒt=9.5mm，葉輪輪(lun)毂半徑Ｒo=10mm，葉(ye)輪輪毂長(zhang)度Lh=8mm，葉輪導(dao)程L=88.5mm，導流體(ti)葉片數N2=4，前(qian)導流體輪(lun)毂長度H1=54mm，後(hou)導流體輪(lun)毂長度H2=38mm。按(an)照上述幾(ji)何參數建(jian)立三維模(mo)型，如圖1所(suo)示。爲了使(shi)流體接近(jin)充分發展(zhan)狀态從而(er)形成穩定(ding)的流速分(fen)布，在渦輪(lun)流量計前(qian)後分别加(jia)裝10D和5D長直(zhi)管段［10］。

1.2網格劃分(fen)
　　将三維模(mo)型導入網(wang)格劃分軟(ruan)件ICEM中，考慮(lü)圖1渦輪流(liu)量計三維(wei)模型Fig．13Dmodeloftheturbineflowmeter到流(liu)量計葉輪(lun)部分和導(dao)流件部分(fen)結構複雜(za)，而且是仿(pang)真計算的(de)關鍵部件(jian)，因此在ICEM中(zhong)均采用非(fei)結構化的(de)四面體網(wang)格對葉輪(lun)流域和導(dao)流件流域(yu)進行劃分(fen);而前、後直(zhi)管段流域(yu)結構相對(dui)簡單但尺(chi)寸較大，采(cai)用四面體(ti)網格劃分(fen)會使網格(ge)數量大大(da)增加，爲了(le)減少仿真(zhen)時間，采用(yong)結構化的(de)六面體網(wang)格對該流(liu)域進行劃(hua)分，劃分後(hou)的網格數(shu)爲1474621個，其Quali-ty最(zui)小值爲0.36。通(tong)過增加整(zheng)體網格數(shu)進行網格(ge)無關性檢(jian)驗，網格尺(chi)度符合計(ji)算要求。
1.3邊(bian)界條件定(ding)義
邊界條(tiao)件如下:
(1)仿(pang)真介質采(cai)用實際狀(zhuang)況下的原(yuan)油，其運動(dong)黏度爲2.64×10-5m2/s，密(mi)度爲887kg/m3，流量(liang)範圍2～20m3/h;
(2)入口(kou)采用速度(du)入口，選取(qu)2m3/h、4m3/h、8m3/h、14m3/h、20m3/h這5個體積(ji)流量下的(de)入口速度(du);出口采用(yong)壓力出口(kou)，設置爲1個(ge)标準大氣(qi)壓;
(3)管壁，上(shang)、下導流體(ti)和葉輪表(biao)面均采用(yong)無滑移壁(bi)面邊界條(tiao)件;
(4)渦輪流(liu)量計葉輪(lun)部分流域(yu)設置爲旋(xuan)轉流域，前(qian)後導流件(jian)部分設置(zhi)爲固定流(liu)域，旋轉流(liu)域與固定(ding)流域之間(jian)采用交界(jie)面進行連(lian)接。
1.4湍流模(mo)型的選擇(ze)
　　由于渦輪(lun)流量計葉(ye)輪在流體(ti)中處于高(gao)速旋轉狀(zhuang)态，其表面(mian)曲率變化(hua)非常大，而(er)雷諾應力(li)模型(ＲSM)考慮(lü)到了流體(ti)旋轉或流(liu)線彎曲所(suo)帶來的應(ying)力張量的(de)急劇變化(hua)，可以更好(hao)地模拟渦(wo)輪流量計(ji)在複雜流(liu)場狀況下(xia)的運行規(gui)律，因此選(xuan)用ＲSM湍流模(mo)型［11］。
1.5仿真儀(yi)表系數和(he)線性度誤(wu)差的計算(suan)
　　儀表系數(shu)爲渦輪感(gan)應放大器(qi)産生的脈(mo)沖數與流(liu)過傳感器(qi)流體體積(ji)的比值［12］。在(zai)計算仿真(zhen)儀表系數(shu)之前需要(yao)計算流量(liang)計葉輪在(zai)該流量下(xia)的穩定轉(zhuan)速θ。通過監(jian)測發現，當(dang)葉輪驅動(dong)力矩與阻(zu)力矩的差(cha)值小于10-8時(shi)，可認爲葉(ye)輪所受力(li)矩達到平(ping)衡，則此時(shi)的葉輪轉(zhuan)速即爲穩(wen)定轉速。葉(ye)輪穩定轉(zhuan)速确定後(hou)，根據葉片(pian)個數、入口(kou)流速與管(guan)道截面積(ji)可以得到(dao)此時的渦(wo)輪流量計(ji)仿真儀表(biao)系數，其計(ji)算公式爲(wei)

　　式中,K爲渦(wo)輪流量計(ji)仿真儀表(biao)系數,L-1;N爲葉(ye)輪葉片個(ge)數;?爲葉輪(lun)穩定轉速(su),rad/s;V爲入口流(liu)速，m/s;A爲前直(zhi)管段入口(kou)截面積,m2
　　儀(yi)表系數線(xian)性度誤差(cha)可以反映(ying)渦輪流量(liang)計的測量(liang)精度，儀表(biao)系數線性(xing)度誤差越(yue)小，則流量(liang)計的測量(liang)精度越高(gao),反之則測(ce)量精度越(yue)低。
　　通過式(shi)(1)計算出2m3/h、4m3/h、8m3/h、14m3/h、20m3/h這(zhe)5個點的仿(pang)真儀表系(xi)數後，便可(ke)以得到渦(wo)輪流量計(ji)儀表系數(shu)線性度誤(wu)差8,其計算(suan)公式爲

　　式(shi)中Kmin,i爲流量(liang)計在5個流(liu)量點處得(de)到的儀表(biao)系數最大(da)值;Kmin,i，爲流量(liang)計在5個流(liu)量點處得(de)到的儀表(biao)系數最小(xiao)值。
2Plackett-Burman設計
　　根(gen)據.Plackett-Burman(PB)試驗設(she)計，選取8個(ge)試驗因素(su)(葉輪頂端(duan)半徑、葉輪(lun)葉片數、葉(ye)輪輪毂半(ban)徑、葉輪輪(lun)毂長度、葉(ye)輪導程、前(qian)導流件長(zhang)度、後導流(liu)件長度、導(dao)流體葉片(pian)數)和3個空(kong)白因素,每(mei)個因素設(she)高、低兩個(ge)水平，以儀(yi)表系數線(xian)性度誤差(cha)爲響應值(zhi),共計12個試(shi)驗，試驗設(she)計因素及(ji)水平見表(biao)1。

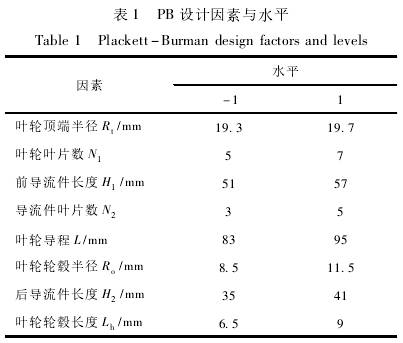
　　對表1試驗(yan)中各因素(su)進行顯著(zhe)性分析，分(fen)析結果如(ru)表2所示，模(mo)型顯著差(cha)異水平p=0.004,說(shuo)明.回歸方(fang)程關系顯(xian)著;決定系(xi)數R2=0.9927,說明回(hui)歸有效,試(shi)驗結果可(ke)靠。由表2還(hai)可以看出(chu)8個因素均(jun)對流量計(ji)線性度誤(wu)差影響顯(xian)著,其中葉(ye)輪葉片數(shu)N1、葉輪頂端(duan)半徑R1、葉片(pian)輪毂半徑(jing)R.。、葉輪輪毂(gu)長度Lh這4個(ge)爲顯著影(ying)響參數,在(zai)後文中運(yun)用響應面(mian)法進行優(you)化;而葉輪(lun)導程L、前導(dao)流件長度(du)H1、後導流件(jian)長度H2、導流(liu)體葉片數(shu)N2這4個爲次(ci)顯著影響(xiang)參數,在後(hou)文中運用(yong)正交試驗(yan)進行優化(hua)。

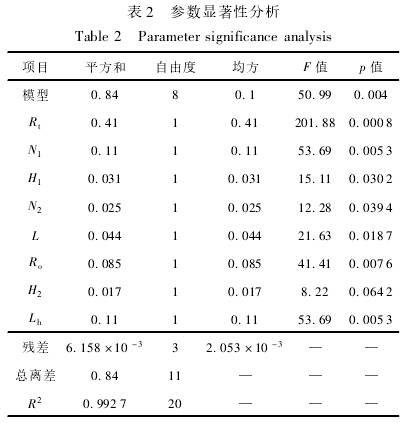
3結構參數(shu)優化.
3.1顯著(zhe)影響參數(shu)的響應面(mian)法優化
　　采(cai)用Box-Behnken中心組(zu)合設計方(fang)法，以葉輪(lun)頂端半徑(jing)Rt、葉片數N1、葉(ye)片輪毂半(ban)徑R.。、葉輪輪(lun)毂長度Lh這(zhe)4個顯著影(ying)響因素爲(wei)自變量,儀(yi)表系數線(xian)性度誤差(cha)爲響應值(zhi),其餘結構(gou)參數保持(chi)不變,設計(ji)四因素三(san)水平29個試(shi)驗點的響(xiang)應面優化(hua)試驗。因素(su)與水平見(jian)表3,試驗設(she)計見表4。

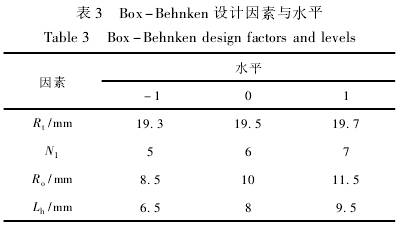
對(dui)模型進行(hang)方差分析(xi)得到的響(xiang)應面分析(xi)結果如

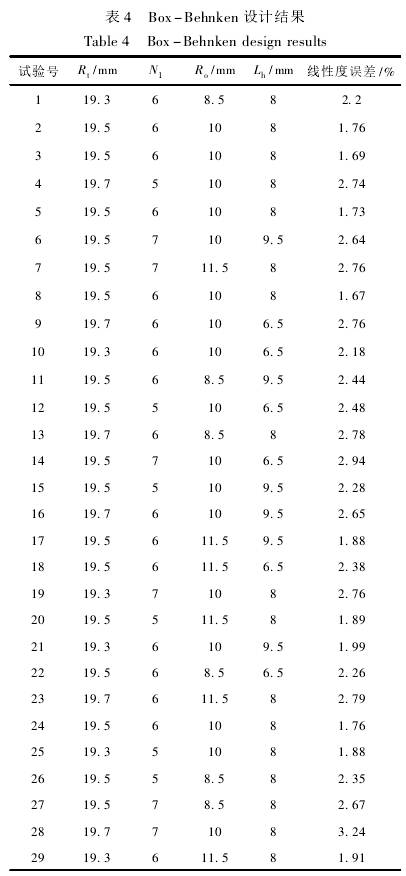
　　表(biao)5所示,p<0.0001<0.05,表明(ming)該模型是(shi)顯著的，具(ju)有統計學(xue)意義。由表(biao)5數據可得(de),自變量R、N、R。、Lh均(jun)顯著(p<0.05),按照(zhao)對響應值(zhi)的影響程(cheng)度排序爲(wei)葉輪頂端(duan)半徑R1>葉輪(lun)葉片數N1>葉(ye)輪輪毂長(zhang)度Lh>葉輪輪(lun)毂半徑R。失(shi)拟項P=0.056>0.05,此值(zhi)不顯著,說(shuo)明在試驗(yan)範圍内預(yu)測值和實(shi)測值的拟(ni)合度較高(gao)，能夠選擇(ze)該回歸方(fang)程對試驗(yan)結果進行(hang)相關分析(xi)，線性度誤(wu)差R的回歸(gui)方程爲
R=17.22+3.37Rt+2.82N1-0.91R。-0.93Lh-0.95RtN1+0.75R1R。+0.2R1Lh+1.38N1R。-0.25N1Lh-1.70R。Lh+4.22R21+5.16N21+2.26R2。+2.97Lh2


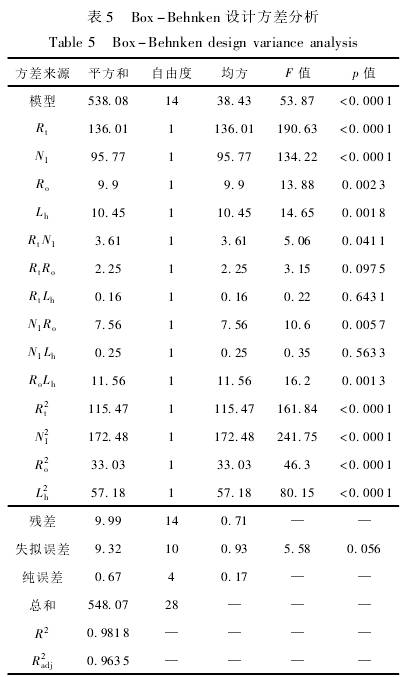
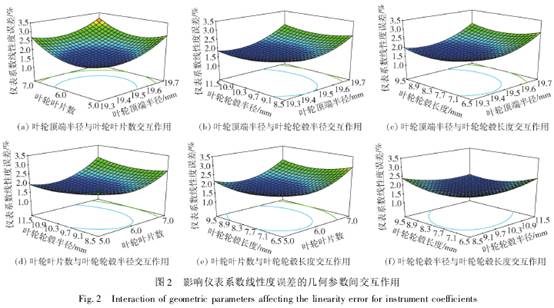
　　從(cong)圖2(a)~(f)可形象(xiang)地看出影(ying)響儀表系(xi)數線性度(du)誤差的幾(ji)何參數間(jian)交互作用(yong)。比較圖2各(ge)個分圖可(ke)知,葉輪頂(ding)端半徑R1對(dui)儀表系數(shu)線性度誤(wu)差的影響(xiang)最爲顯著(zhe)，表現爲曲(qu)線最陡，其(qi)餘因素影(ying)響大小順(shun)序爲葉輪(lun)葉片數N1>葉(ye)輪輪毂長(zhang)度Lh>葉輪輪(lun)毂半徑R。這(zhe)也與表5的(de)方差分析(xi)結果相吻(wen)合。
　　使用DesignExpert軟(ruan)件在表3變(bian)量的高低(di)水平範圍(wei)内尋優,以(yi)葉輪葉片(pian)數是整數(shu)爲前提，取(qu)其中一個(ge)最優組合(he)進行CFD仿真(zhen)計算,并與(yu)顯著因素(su)的響應面(mian)回歸方程(cheng)預測值進(jin)行比較,比(bi)較結果如(ru)表6所示。可(ke)以看出，對(dui)于優化後(hou)的流量計(ji)模型,其儀(yi)表系數線(xian)性度誤差(cha)拟合公式(shi)的預測值(zhi)與CFD計算值(zhi)非常接近(jin),誤差僅爲(wei)0.6%,說明響應(ying)面法可以(yi)很好地用(yong)于渦輪流(liu)量計結構(gou)優化。
3.2次顯(xian)著影響參(can)數的正交(jiao)試驗設計(ji)
　　在對顯著(zhe)參數進行(hang)響應面優(you)化後,選擇(ze)葉輪導程(cheng)L、前導流件(jian)長度H、導流(liu)體葉片數(shu)N2、後導流件(jian)長度H2這4個(ge)次顯著影(ying)響因素爲(wei)自變量,以(yi)流量計線(xian)性，度誤差(cha)爲響應值(zhi)進行正交(jiao)試驗設計(ji),根據因素(su)和水平數(shu)選擇正交(jiao)表L9(34),一共9組(zu)仿真計算(suan)模型,因素(su)與水平見(jian)表7。
　　正交試(shi)驗結果與(yu)均值如表(biao)8所示,因素(su)L對應的均(jun)值2最小,表(biao)明L取第二(er)水平上的(de)值時線性(xing)度誤差最(zui)小，同理可(ke)以得到H1、N2和(he)H2的取值分(fen)别爲:
　　第三(san)水平、第二(er)水平和第(di)二水平,因(yin)此理論上(shang)的最優水(shui)平組合爲(wei)L2(H)3(N2)2(H2)22。

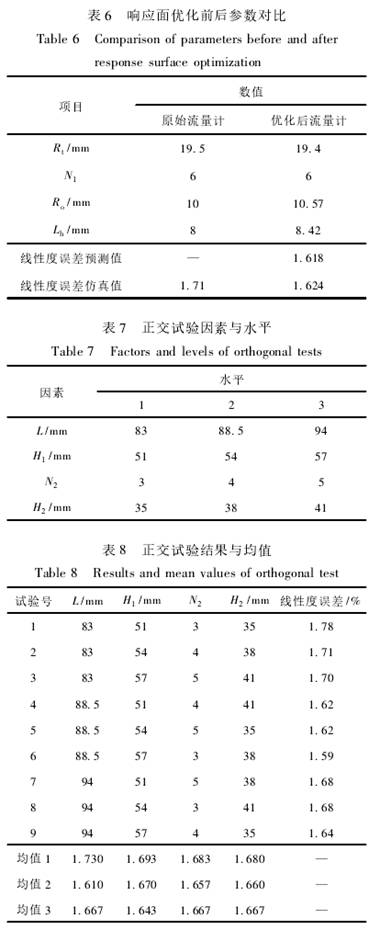
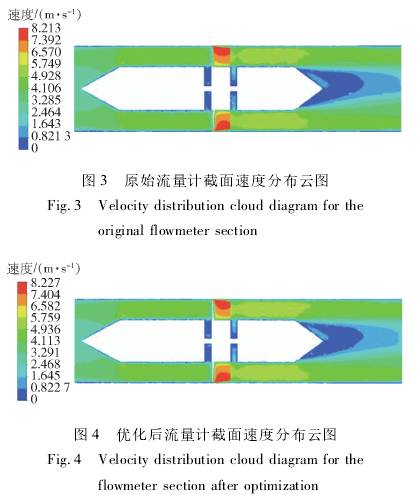
　　圖3和圖4分(fen)别爲原始(shi)流量計與(yu)優化後流(liu)量計的截(jie)面速度分(fen)布雲圖。對(dui)比圖3和圖(tu)4可以看出(chu)，優化後的(de)流量計在(zai)後導流件(jian).上下部分(fen)的流場速(su)度分布較(jiao)原始流量(liang)計更加均(jun)勻,說明優(you)化後流量(liang)計的葉輪(lun)結構在流(liu)場中的旋(xuan)轉穩定性(xing)更好,從而(er)使得測量(liang)精度得到(dao)提高。

4試驗(yan)驗證
　　将優(you)化前後的(de)渦輪流量(liang)計在流量(liang)技術檢測(ce)試驗台。上(shang)進行試驗(yan)，試驗裝置(zhi)如圖5所示(shi)。試驗介質(zhi)采用由機(ji)油和柴油(you)按照一定(ding)比例混合(he)的密度爲(wei)887kg/m3、運動黏度(du)爲2.64×10-5m2/s的混合(he)液,采用靜(jing)态容積法(fa)原理,利用(yong)泵爲流體(ti)提供動力(li),流體經過(guo)流量控制(zhi)閥和被測(ce)渦輪流量(liang)計後直接(jie)流回容積(ji)池中。分别(bie)選取2m3/h、4m3/h、8m3/h、14m3/h、16m3/h、20m3/h這6個(ge)體積流量(liang)點,通過計(ji)算機控制(zhi)台采集每(mei)個流量點(dian)下試驗流(liu)量計産生(sheng)的脈沖個(ge)數N,從而得(de)到渦輪流(liu)量計在6個(ge)流量點下(xia)的儀表系(xi)數K。試驗中(zhong)每個流量(liang)點分别進(jin)行3次重複(fu)性試驗，試(shi)驗誤差均(jun)小于0.025%。

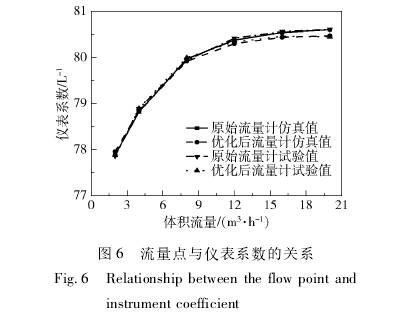
　　将原(yuan)始流量計(ji)儀表系數(shu)與優化後(hou)的流量計(ji)儀.表系數(shu)進行對比(bi)，結果如圖(tu)6所示。流量(liang)計儀表系(xi)數CFD仿真值(zhi)與試驗值(zhi)吻合,證明(ming)了CFD仿真的(de)準确性。對(dui)比原始渦(wo)輪流量計(ji)和優化後(hou)渦輪流量(liang)計儀表系(xi)數試驗值(zhi)曲線得出(chu),優化後的(de)流量計在(zai)不同流量(liang)處的儀表(biao)系數變化(hua)情況較原(yuan)來更爲平(ping)穩。經計算(suan)，儀表系數(shu)線性度誤(wu)差由原來(lai)的1.71%下降到(dao)了1.59%，顯著提(ti)高了渦輪(lun)流量計的(de)測量精度(du)。

5結論
(1)Plackett-Burman設計(ji)分析表明(ming)，對渦輪流(liu)量計測量(liang)精度影響(xiang)顯著的參(can)數爲葉輪(lun)頂端半徑(jing)、葉輪葉片(pian)數、葉輪輪(lun)毂半徑和(he)葉輪輪毂(gu)長度,影響(xiang)次顯著的(de)參數有葉(ye)輪導程、前(qian)導流件長(zhang)度、後導流(liu)件長度和(he)導流體葉(ye)片數。
(2)運用(yong)Box-Behnken設計方法(fa)對篩選出(chu)來的顯著(zhe)影響參數(shu)進行試驗(yan)設計，建立(li)了渦輪流(liu)量計線性(xing)度誤差的(de)多元回歸(gui)模型,并檢(jian)驗了預測(ce)模型的拟(ni)合度。結果(guo)表明,回歸(gui)模型對實(shi)際情況拟(ni)合較好，能(neng)夠運用響(xiang)應面法對(dui)渦輪流量(liang)計結構參(can)數進行優(you)化。
(3)在響應(ying)面法優化(hua)的基礎上(shang),對篩選出(chu)來的次顯(xian)著影響參(can)數進行正(zheng)交試驗設(she)計,得到了(le)最優結構(gou)組合。試驗(yan)驗證結果(guo)表明優化(hua)後的渦輪(lun)流量計測(ce)量精度得(de)到了顯著(zhe)提高。

以上(shang)内容源于(yu)網絡，如有(you)侵權聯系(xi)即删除!