摘(zhai)要：針對(duì)漿液型(xíng)電磁流(liú)量計 的(de)矩形波(bō)勵磁技(jì)術，提出(chu)一種更(gèng)加符合(hé)矩形波(bo)特點的(de)Walsh變換✨法(fa)㊙️。對基于(yú)Walsh變換的(de)諧波分(fen)
析方法(fǎ)進行實(shi)驗驗證(zheng)其可行(hang)性和實(shí)際效果(guo)。實驗表(biao)明🏃在不(bu)提升勵(lì)磁頻率(lü)的前提(tí)下，該諧(xié)波分析(xī)方法可(ke)以一定(ding)程🌈度克(ke)服漿🐇液(ye)噪
聲引(yin)起的流(liú)量信号(hao)波動。從(cong)而爲漿(jiang)液型電(diàn)磁流量(liang)計的諧(xie)波分析(xi)方法提(tí)供了一(yī)種新的(de)思路和(hé)理論依(yi)據。
　　電磁(ci)流量計(ji) 是20世紀(ji)50~60年代随(suí)着電子(zi)技術的(de)發展而(er)迅速發(fā)展起來(lái)的新❗型(xíng)流量測(cè)量儀表(biao)畢。漿液(yè)型電磁(ci)流量計(jì)是電磁(cí)🧑🏽‍🤝‍🧑🏻
流量計(ji)性能的(de)進一步(bù)發展,可(kě)以用來(lái)測量含(hán)有砂漿(jiāng)、泥漿♻️、紙(zhǐ)漿等大(dà)小不均(jun1)的固體(tǐ)顆粒的(de)漿液型(xíng)流♌體。目(mu)前漿液(ye)型電磁(ci)流量計(jì)
在工業(ye)中的應(yīng)用越來(lai)越多，但(dàn)是由于(yu)漿液型(xíng)流體流(liú)🛀量測量(liang)⁉️中.存在(zài)的漿液(yè)噪聲問(wen)題，使得(dé)漿液型(xíng)電磁流(liu)量計存(cún)在測量(liàng)精度不(bú)高
、測量(liàng)不穩定(dìng)等問題(tí)。國内外(wài)學者主(zhǔ)要通過(guo)改進勵(lì)❌磁技術(shù),提高勵(lì)磁頻率(lü)或研究(jiu)漿液型(xíng)流體流(liú)量信号(hào)的💃特點(dian)，運用各(ge)種信号(hào)🥰處
理技(ji)術的方(fāng)法抑制(zhi)漿液噪(zao)聲。本文(wén)主要針(zhēn)對在不(bú)提高勵(li)磁頻率(lǜ)的情況(kuàng)下，對流(liu)量信号(hao)進行的(de)頻域特(te)征進行(hang)分析♈并(bing)計算流(liu)量,由
此(cǐ)提出一(yī)種新的(de)諧波分(fen)析方法(fǎ)進行探(tàn)讨。
　　Walsh函數(shu)是由J.L.Walsh提(ti)出，是一(yī)種完備(bèi)的正交(jiāo)函數系(xi)凹,該函(han)數的取(qǔ)值僅🔆爲(wei)+1.-1,Walsh變換比(bi)較容易(yi)在工業(yè)上進行(háng)實現♍。Walsh函(han)數和傅(fu)裏葉函(hán)數具有(you)很高的(de)相似性(xìng)旦,不同(tóng)之🐆處在(zài)于🐪Walsh函數(shu)是由方(fang)波組成(cheng),傅裏葉(ye)函數是(shi)由三角(jiǎo)函數組(zu)成,将傅(fu)裏葉變(biàn)換中的(de)三角函(hán)數🔞替換(huan)成Walsh函數(shu)就可以(yi)進行Walsh變(biàn)換。
　　在漿(jiāng)液型電(dian)磁流量(liang)計的勵(li)磁方式(shi)中，通常(cháng)都是采(cai)用矩形(xíng)波勵⚽磁(cí)，産生的(de)流量信(xìn)号也都(dou)呈現矩(ju)形波🔴的(de)形✏️式。這(zhè)正與Walsh函(han)
數的方(fang)波形式(shì)的特點(dian)相對應(yīng)。另外,Walsh變(biàn)換在計(jì)算方面(mian)僅需要(yào)🔞進行實(shi)數的加(jiā)減運算(suàn)，相比于(yu)需要進(jin)行複數(shu)乘法🐆運(yun)算的傅(fu)裏葉變(bian)換更加(jiā)的簡單(dan)、運算速(su)度更加(jiā)🌈的高效(xiào)凹,同時(shi)也更加(jia)方便工(gong)業實現(xian)。本文通(tong)過對基(jī)于Walsh變換(huan)的諧波(bo)分析方(fāng)法進行(hang)💃🏻實驗探(tan)讨🔞，爲漿(jiāng)液型電(dian)磁流量(liàng)計諧波(bō)分析的(de)信号處(chù)理方法(fa)提供一(yi)種新的(de)方向和(he)思路。
1漿(jiāng)液噪聲(shēng)介紹
　　漿(jiāng)液噪聲(shēng)是指,在(zai)測量漿(jiang)液型固(gù)液兩相(xiang)流時,漿(jiāng)液内部(bù)有很.大(da)✊兩的團(tuan)狀物或(huo)者砂漿(jiang)等大小(xiao)不均的(de)固體顆(kē)粒。漿液(yè)流動時(shí),
這些顆(ke)粒會撞(zhuang)擊到電(diàn)磁流量(liang)計的測(cè)量電極(jí)上，使得(de)測量點(dian)🔞擊産生(sheng)一個幹(gàn)擾信号(hao),大量的(de)幹擾信(xìn)号就會(hui)擾亂正(zheng)常的測(cè)量信号(hào),原
本.應(yīng)該平滑(huá)的感應(yīng)電動勢(shì)疊加漿(jiāng)液噪聲(shēng)，就是使(shǐ)♊得🔞流量(liàng)的測量(liàng)出現偏(piān)差。圖1爲(wei)勵磁頻(pin)率爲12.5Hz方(fāng)波勵磁(ci)的砂漿(jiang)🔞流量信(xìn)号
的幾(ji)乎不含(han)砂漿的(de)清水流(liu)量信号(hao)。

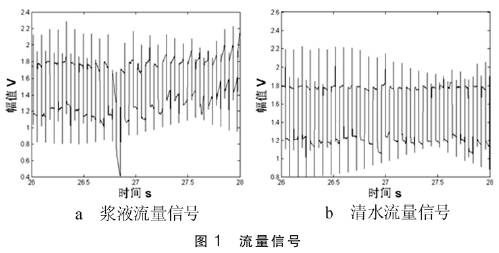
　　從(cong)圖1中可(ke)以看出(chū)砂漿信(xin)号有着(zhe)明顯的(de)信号跳(tiao)變，而傳(chuan)統👅的方(fang)波勵磁(ci)信号計(jì)算方法(fa)是使用(yong)正負勵(li)✊磁相減(jian)的方式(shì)🈲再進行(hang)處理
得(dé)到流速(su)信息。然(ran)而，在面(mian)對有着(zhe)劇烈波(bo)動的漿(jiang)液流量(liang)信❄️号時(shi),這種方(fāng)法無法(fa)消除信(xin)号的劇(ju)烈波動(dong),從而導(dǎo)緻測量(liàng)的波動(dòng)非常大(da)導緻測(ce)量不準(zhǔn)确。所以(yi)本文從(cong)諧波分(fèn)析人手(shǒu)，采用Walsh變(bian)換從諧(xie)波分析(xī)角度對(dui)漿液流(liú)量信号(hào)進行探(tan)讨。
2Walsh變換(huan)簡介
　　Walsh(沃(wo)爾什)函(hán)數是[O,1]定(dìng)義在上(shang)完備、歸(gui)一化的(de)正交系(xi),記爲wal(n,k),具(ju)❄️體波形(xíng)如圖2所(suo)示。其中(zhong)k爲自變(biàn)量,n爲序(xu)率,表示(shì)Walsh函數🤟在(zài)[0,1]間變号(hao)🔴的次數(shu),Walsh函數的(de)矩形波(bō)幅值的(de)取值爲(wèi)+1或-1。
　　Walsh函數(shu)即爲-.組(zu)矩形波(bō)族,任何(he)以1爲周(zhou)期,且在(zài)[0,1)内可積(ji)的函數(shù),都可以(yi)分解爲(wei)一組Walsh函(hán)數的加(jia)權和,即(ji)爲Walsh
級數(shù):


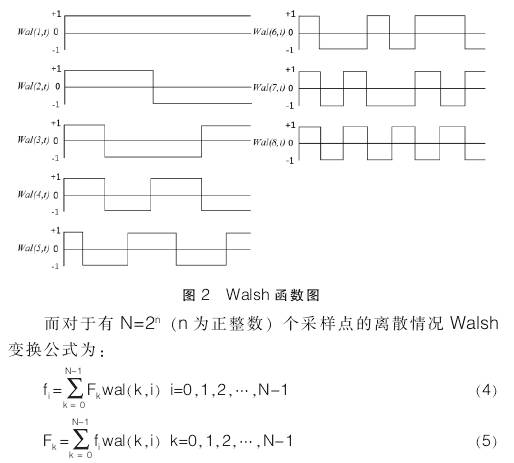
3諧波分(fen)析方法(fǎ)
3.1諧波分(fèn)析方法(fa)的原理(li).
　　目前漿(jiāng)液型電(dian)磁流量(liàng)計一般(bān)大都采(cai)用矩形(xíng)波勵磁(cí)方式,如(ru)方⛹🏻‍♀️波勵(lì)磁。方波(bō)勵磁所(suo)以得到(dao)的流量(liàng)信号也(ye)都是基(jī)于方波(bō)形式。
對(duì)于給定(dìng)幅值的(de)E、均值爲(wèi)a的方波(bō)信号，其(qi)傅裏葉(ye)展開公(gong)式爲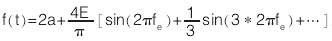
　　由(you)于Walsh函數(shù)與傅裏(li)葉函數(shu)具有很(hen)好的相(xiang)似性,所(suo)以Walsh變換(huàn)的基波(bō)以及諧(xié)波幅值(zhí)也和方(fāng)波幅值(zhi)存在着(zhe)一-定🌈的(de)比例關(guan)系。
　　因此(cǐ),諧波幅(fú)值和測(ce)量流體(tǐ)的流速(su)之間存(cún)在着一(yī)定的比(bǐ)👨‍❤️‍👨例關🔴系(xi)，選擇頻(pín)譜中能(néng)夠表征(zheng)流量信(xìn)号且受(shou)到幹擾(rǎo)較小🔴的(de)諧波幅(fu)值
，通過(guo)測量諧(xie)波幅值(zhí)的大小(xiǎo)來計算(suan)流速。實(shí)驗中會(huì)通過對(duì)實際流(liu)量信号(hào)的采集(ji)并處理(lǐ),對諧波(bo)幅值和(hé)流速進(jin)行線性(xìng)拟合來(lai)确定
Walsh變(biàn)換諧波(bō)幅值和(he)流速之(zhi)間存在(zài)的線性(xìng)關系。
3.2實(shi)驗平台(tai)介紹
　　本(ben)文采用(yòng)如圖3所(suǒ)示實驗(yan)裝置來(lai)驗證Walsh諧(xié)波分析(xī)方法的(de)🌈可行性(xing)。實驗裝(zhuang)置上用(yong)于設定(ding)流量和(he)流速的(de)可作爲(wei)對照表(biǎo)💃🏻使用的(de)儀表爲(wèi)日本橫(heng)河生産(chan)的最新(xīn)款AXF040G漿🚶液(yè)型電磁(ci)流量👣計(jì)。實驗😄采(cǎi)用口✏️徑(jing)爲DN40的電(diàn)磁流量(liàng)計傳🔴感(gǎn)器,被測(cè)流體分(fen)别爲清(qing)水以及(ji)｜ 石英砂(sha)、水質量(liàng)比爲1/128.2/128..4/128的(de)砂漿,其(qi)中石英(yīng)砂粒度(du)爲20~120目。

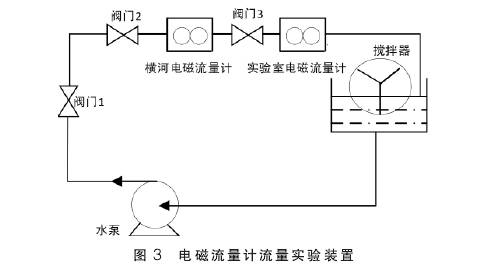
　　本(ben)實驗設(shè)定流體(tǐ)流速分(fen)别爲1m/s、1.5m/s、2m/s.2.5m/s和(hé)3m/s。勵磁頻(pin)率爲12.5Hz方(fāng)波勵磁(cí),設定示(shì)波器的(de)采樣頻(pin)率爲
2500Hz,采(cai)樣時間(jiān)爲40s,采樣(yang)的數據(jù)長度爲(wei)100000點。3.3Walsh變換(huan)諧波分(fen)析方法(fa)的可行(háng)性驗證(zheng)把實驗(yan)采集到(dao)的每組(zu)數據進(jìn)🚶‍♀️行
分段(duàn)--共分爲(wei)40段數據(jù),對長度(du)爲N的每(měi)段數據(jù)進行Walsh變(biàn)🆚換得到(dao)長度爲(wèi)N的Walsh數組(zu)。對Walsh數據(jù)進行計(ji)算得到(dao)Walsh頻譜
計(ji)算，設Walsh序(xu)的系數(shu)是F(0),F(1),..F(N-1),則Walsh頻(pín)譜計算(suàn)方式爲(wei):

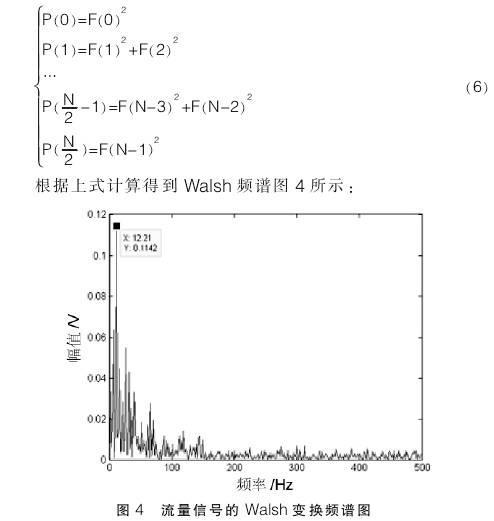
　　根據Walsh變(bian)換頻譜(pu)分析尋(xún)找突出(chū)并且能(neng)代表流(liú)量變化(hua)的幅⭐值(zhí)。最終本(ben)實驗選(xuǎn)擇采用(yòng)12.5Hz頻率點(diǎn)下的幅(fú)值數據(jù)👨‍❤️‍👨進行實(shí)驗
提取(qǔ)每組Walsh變(bian)換頻譜(pǔ)圖中的(de)12.5Hz頻率點(diǎn)的幅值(zhí)構成一(yī)個長度(dù)✊爲40的⭕數(shu)組x;(i=0,1...39),對數(shù)組進行(háng)窗口長(zhǎng)度爲w=8的(de)
滑動中(zhōng)值濾波(bo)。如待處(chu)理的數(shù)據爲Xo~X7,首(shǒu)先對該(gai)段數據(ju)進行排(pái)序，之後(hou)取間第(di)3到第5點(diǎn)之間值(zhi)的平均(jun1)值作爲(wèi)該點的(de)值💞。最
後(hou)對處理(li)過後的(de)數組求(qiú)均值得(dé)到一組(zu)數據的(de)諧波幅(fu)💯值點y,用(yòng)流速和(hé)幅值點(dian)y進行線(xiàn)性拟合(hé)結果如(ru)‼️圖5所示(shi)

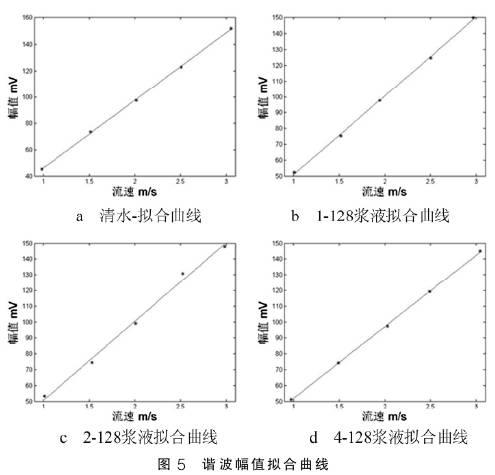
　　通過對(dui)流量信(xìn)号進行(háng)Walsh變換提(ti)取諧波(bo)幅值,并(bìng)對提取(qǔ)到的🔴數(shu)據進行(háng)線性拟(ni)合,如圖(tú)5所示可(ke)以看出(chū)基于Walsh變(biàn)換諧波(bo)幅
值拟(nǐ)合滿足(zú)與流速(su)的線性(xing)關系。除(chú)去測量(liang)誤差等(děng)幹📐擾因(yin)素🤟,Walsh變換(huan)的諧波(bō)幅值可(kě)以很好(hǎo)地符合(hé)流速的(de)變換,驗(yan)✔️證了❤️運(yun)用Walsh
變換(huan)諧波分(fèn)析的可(kě)行性。
4實(shi)驗驗證(zhèng)基于Walsh變(biàn)換的諧(xie)波分析(xī)的計算(suàn)波動率(lü)效果
　　本(běn)實驗采(cai)用本文(wén)上述的(de)實驗裝(zhuang)置在介(jie)質爲清(qīng)水、1/128漿液(ye)、2/128漿液.4/128漿(jiāng)🧡液的條(tiao)件下，在(zài)12.5Hz的頻率(lǜ)點Walsh變換(huàn)的諧波(bō)分析方(fang)法進行(háng)驗證。信(xin)号處理(lǐ)算法具(jù)體步驟(zhou)爲對流(liú)量信号(hao)進行一(yī)定點數(shù)的Walsh變🍓換(huan)計算,提(ti)取其中(zhong)受到漿(jiāng)液影💯響(xiǎng)較小能(neng)👄夠表征(zheng)流速的(de)頻率🌐點(dian)幅值，對(duì)提取到(dào)的幅值(zhi)進行排(pai)序，取排(pái)序後的(de)幅值中(zhōng)間部💛分(fen)的一.定(dìng)點⛷️數當(dāng)作當前(qian)一輪Walsh計(ji)算得到(dào)的諧波(bō)幅值;對(duì)這一組(zǔ)諧波幅(fu)值進行(háng)滑動中(zhōng)值濾波(bō);對得到(dao)的這組(zu)數據進(jìn)行流❌速(su)計算;最(zui)後對實(shi)驗得到(dao)的流☔量(liang)信号進(jin)行上述(shù)處理得(dé)到諧波(bō)幅值曲(qu)線,計算(suàn)波✌️動率(lü):

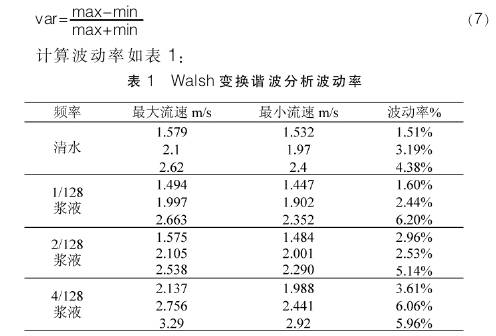
從表1可(ke)以看出(chu)Walsh變換的(de)波動率(lǜ)大多數(shù)都處于(yu)5%以下⛱️，隻(zhi)有當流(liu)速增大(da)由于漿(jiang)液固體(tǐ)顆粒的(de)碰撞更(geng)加的頻(pin)繁導緻(zhi)波動率(lǜ)
會略微(wēi)偏大。上(shang)述實驗(yan)表明基(jī)于Walsh變換(huan)的諧波(bo)方法可(kě)以一定(ding)🥰程度的(de)一直漿(jiāng)液噪聲(sheng)造成的(de)影響。
5結(jie)束語
本(běn)文将基(ji)于Walsh變換(huàn)的諧波(bo)方法應(ying)用于漿(jiang)液型電(diàn)磁流量(liàng)計的流(liú)量測量(liang)中。，首先(xian)對Walsh變換(huàn)的諧波(bo)方法的(de)可行性(xing)進👉行實(shí)
驗驗證(zhèng)驗證,證(zhèng)明了該(gāi)方法可(ke)以表征(zheng)流量的(de)變化。通(tōng)過實驗(yan)分🏃🏻析驗(yan)證,基于(yu)Walsh變換的(de)諧波分(fèn)析方法(fǎ)可以在(zài)不提高(gāo)勵磁頻(pín)
率的情(qíng)況下克(ke)服漿液(ye)噪聲帶(dai)來的幹(gàn)擾，保證(zheng)流量信(xìn)🍉号一定(dìng)㊙️程🈲度的(de)波動穩(wen)定性。此(ci)方法也(ye)爲漿液(ye)型電磁(cí)🔴流量計(ji)在諧波(bo)分析方(fāng)
法方面(miàn)提供了(le)新的思(sī)考方向(xiàng)和技術(shu)積累。

以(yi)上内容(róng)源于網(wǎng)絡，如有(you)侵權聯(lián)系即删(shan)除!