|
多相(xiang)流測(ce)量中(zhong)渦輪(lun)流量(liang)計的(de)影響(xiang)
|
摘要(yao):闡述(shu)了渦(wo)輪流(liu)量計(ji)
的工(gong)作原(yuan)理和(he)動态(tai)特性(xing),建立(li)了渦(wo)輪流(liu)量計(ji)的多(duo)相流(liu)測量(liang)模🌈型(xing),并在(zai)多相(xiang)流模(mo)拟裝(zhuang)置中(zhong)進行(hang)了實(shi)驗驗(yan)✏️證,得(de)出了(le)流體(ti)密度(du)🐇是渦(wo)輪流(liu)量計(ji)在測(ce)量多(duo)相流(liu)的流(liu)量時(shi)的影(ying)響👨❤️👨因(yin)子,并(bing)且讨(tao)論了(le)流體(ti)密度(du)影響(xiang)多相(xiang)流的(de)流量(liang)測量(liang)的規(gui)👣律。
在(zai)油田(tian)生産(chan)過程(cheng)參數(shu)(如溫(wen)度、壓(ya)力等(deng))檢測(ce)中,以(yi)流量(liang)和各(ge)相❤️持(chi)🛀🏻率測(ce)量複(fu)雜,是(shi)較難(nan)測量(liang)的兩(liang)個參(can)數,因(yin)而,引(yin)起了(le)工☎️程(cheng)技術(shu)人♌員(yuan)的興(xing)趣.随(sui)着油(you)田的(de)發🧡展(zhan),被測(ce)對象(xiang)不🔱再(zai)局限(xian)于單(dan)相流(liu),而要(yao)對多(duo)相流(liu)、混👨❤️👨合(he)狀态(tai)的流(liu)量進(jin)行測(ce)量。測(ce)量多(duo)相流(liu)的技(ji)術難(nan)度要(yao)比單(dan)相流(liu)體的(de)正确(que)測量(liang)大的(de)多,知(zhi)道單(dan)相流(liu)體的(de)密度(du)、粘度(du)及測(ce)量裝(zhuang)置的(de)幾何(he)結構(gou),便可(ke)以🥵對(dui)單.相(xiang)流進(jin)行定(ding)量分(fen)析。如(ru)果能(neng)利用(yong)多相(xiang)流中(zhong)每一(yi)相的(de)上述(shu)各物(wu)理量(liang)對多(duo)相流(liu)進行(hang)測量(liang)的話(hua),就很(hen)方便(bian)。但很(hen)遺憾(han)的是(shi),多相(xiang)流體(ti)的特(te)性遠(yuan)比單(dan)相流(liu)體🐉的(de)特性(xing)複雜(za)的多(duo),如各(ge)組分(fen)之間(jian)不能(neng)均勻(yun)混合(he)、混🏃♂️合(he)流體(ti)的異(yi)常性(xing)、流型(xing)轉變(bian),相對(dui)速度(du)、流體(ti)性質(zhi)、管道(dao)結構(gou)、流動(dong)方向(xiang)等因(yin)素将(jiang)導緻(zhi)渦輪(lun)流量(liang)傳感(gan)器響(xiang)應特(te)性的(de)改變(bian)"
在單(dan)相流(liu)的條(tiao)件下(xia),渦輪(lun)的轉(zhuan)速和(he)流經(jing)它的(de)體積(ji)流量(liang)成一(yi)🏃♀️單值(zhi)線性(xing)函數(shu),在油(you)水兩(liang)相流(liu)中,隻(zhi)要流(liu)量超(chao)過始(shi)動流(liu)量,在(zai)🐇允許(xu)的誤(wu)差範(fan)圍内(nei),渦輪(lun)的響(xiang)應和(he)體積(ji)流量(liang)也是(shi)成線(xian)性函(han)數。
但(dan)在多(duo)相流(liu)動中(zhong),即使(shi)在總(zong)流量(liang)保持(chi)不變(bian)的情(qing)況下(xia),混合(he)流體(ti)的密(mi)度發(fa)生變(bian)化,也(ye)會引(yin)起渦(wo)輪轉(zhuan)速的(de)很♊大(da)變化(hua)。本文(wen)就此(ci)問題(ti),通過(guo)對渦(wo)輪流(liu)量計(ji)的工(gong)作原(yuan)理和(he)特⛱️性(xing)分析(xi),闡述(shu)了在(zai)測量(liang)👄多相(xiang)流時(shi)的流(liu)量影(ying)響🧑🏽🤝🧑🏻因(yin)子,并(bing)進行(hang)了實(shi)驗驗(yan)證。
1工(gong)作原(yuan)理及(ji)數學(xue)模型(xing)建立(li)
渦輪(lun)流量(liang)計是(shi)一種(zhong)速度(du)式儀(yi)表,它(ta)是以(yi)動量(liang)矩守(shou)恒原(yuan)📧理爲(wei)基礎(chu)的,流(liu)體沖(chong)擊渦(wo)輪葉(ye)片,使(shi)渦輪(lun)旋轉(zhuan),渦輪(lun)的旋(xuan)轉速(su)♊度随(sui)流量(liang)♉的變(bian)化而(er)變化(hua),最後(hou)從渦(wo)⭐.輪的(de)轉數(shu)求出(chu)流量(liang)值,通(tong)過磁(ci)電轉(zhuan)換裝(zhuang)置(或(huo)機械(xie)輸出(chu)裝置(zhi))将渦(wo)輪轉(zhuan)速變(bian)化成(cheng)電脈(mo)沖,送(song)‼️入二(er)次儀(yi)👨❤️👨表進(jin)行計(ji)算和(he)顯示(shi),由單(dan)位時(shi)間電(dian)脈沖(chong)數和(he)累計(ji)電脈(mo)沖數(shu)反映(ying)出瞬(shun)時流(liu)量和(he)累計(ji)流量(liang)(見圖(tu)1)
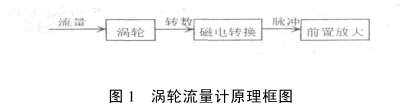
所(suo)以,由(you)動量(liang)矩定(ding)理可(ke)知,渦(wo)輪的(de)運動(dong)微分(fen)方程(cheng)爲🥰:

式(shi)中:J爲(wei)渦輪(lun)的轉(zhuan)動慣(guan)量;w爲(wei)渦輪(lun)的旋(xuan)轉角(jiao)速度(du);∑M爲作(zuo)用在(zai)渦輪(lun)上的(de)合力(li)矩。
在(zai)正常(chang)工作(zuo)條件(jian)下,可(ke)認爲(wei)管道(dao)内的(de)流體(ti)流量(liang)不♉随(sui)時間(jian)變化(hua),即渦(wo)輪以(yi)恒定(ding)的角(jiao)速度(du)ω旋轉(zhuan),這樣(yang)就有(you)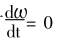
那麽(me)渦輪(lun)的運(yun)動微(wei)分方(fang)程變(bian)爲:
∑M=M-∑Mi=0,(2)
這(zhe)裏把(ba)∑M分成(cheng)了兩(liang)部分(fen),即驅(qu)動渦(wo)輪旋(xuan)轉的(de)驅動(dong)力矩(ju)M和阻(zu)礙渦(wo)輪旋(xuan)轉的(de)各種(zhong)阻力(li)矩∑Mi。通(tong)過分(fen)析計(ji)算♈,驅(qu)動🙇♀️力(li)矩爲(wei)
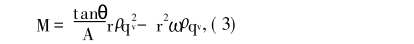
式中(zhong):θ爲葉(ye)片與(yu)軸線(xian)之間(jian)的夾(jia)角;r爲(wei)渦輪(lun)平均(jun)半徑(jing);A爲管(guan)⭐道流(liu)通面(mian)積;ρ爲(wei)流體(ti)密度(du);ω爲渦(wo)輪的(de)旋轉(zhuan)角速(su)度;qv爲(wei)通過(guo)♉管道(dao)的流(liu)量。
将(jiang)式(3)代(dai)入(2)中(zhong)得:

2渦(wo)輪流(liu)量計(ji)的特(te)性分(fen)析
由(you)式(5)和(he)式(6)可(ke)見:當(dang)流體(ti)的粘(zhan)度增(zeng)大時(shi),渦輪(lun)的轉(zhuan)動角(jiao)速度(du)變小(xiao);當流(liu)體密(mi)度變(bian)大時(shi),渦輪(lun)的轉(zhuan)動角(jiao)速度(du)也随(sui)之增(zeng)大。在(zai)流體(ti)速度(du)較小(xiao)(相當(dang)于層(ceng)流狀(zhuang)态)時(shi),渦輪(lun)‼️的頻(pin)率響(xiang)應非(fei)線性(xing),且🌈受(shou)流體(ti)性質(zhi)變化(hua)影響(xiang)較大(da);當流(liu)體速(su)度較(jiao)高(相(xiang)當🈲于(yu)湍流(liu)狀态(tai))時,式(shi)變☔小(xiao),渦輪(lun)響應(ying)💃近似(si)線性(xing),儀🍓器(qi)常數(shu)K基本(ben)上不(bu)受流(liu)體粘(zhan)度變(bian)化影(ying)響。
渦(wo)輪啓(qi)動時(shi),要克(ke)服較(jiao)大的(de)機械(xie)靜摩(mo)擦力(li),因此(ci)需要(yao)較大(da)始動(dong)流量(liang)。渦輪(lun)以--定(ding)的速(su)度轉(zhuan)動起(qi)來以(yi)後,需(xu)要機(ji)械🏃♂️動(dong)摩擦(ca)力和(he)流體(ti)流動(dong)阻力(li),轉動(dong)阈值(zhi)qVmin與p0.5成(cheng)反比(bi),流體(ti)密度(du)越大(da),qVmin越小(xiao)。這🈲種(zhong)情況(kuang)對于(yu)密度(du)變化(hua)小的(de)液🈲體(ti)來說(shuo),影響(xiang)不大(da),可視(shi)爲常(chang)數♍。但(dan)對于(yu)多相(xiang)流體(ti)來說(shuo),由于(yu)溫度(du)、壓力(li)和分(fen)相含(han)率的(de)變化(hua),引起(qi)p變化(hua),從而(er)影響(xiang)qVmin。
3實驗(yan)結果(guo)分析(xi)
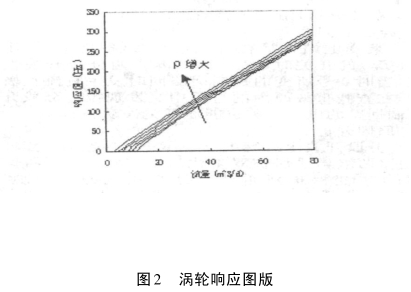
實驗(yan)在以(yi)水和(he)空氣(qi)爲介(jie)質的(de)流動(dong)模拟(ni)裝置(zhi)中進(jin)🈲行,實(shi)驗中(zhong)在氣(qi)體流(liu)量固(gu)定的(de)前提(ti)下,逐(zhu)漸增(zeng)大水(shui)的流(liu)量,測(ce)量渦(wo)輪的(de)響應(ying)值。增(zeng)大氣(qi)體的(de)流量(liang),複上(shang)☂️述操(cao)作,得(de)到了(le)下面(mian)的渦(wo)輪響(xiang)應圖(tu)版,其(qi)中流(liu)量爲(wei)氣液(ye)的合(he)流量(liang)。圖中(zhong)氣體(ti)流量(liang)爲零(ling)時,流(liu)🚶體的(de)密度(du)最大(da),測得(de)的響(xiang)應曲(qu)線各(ge)🈲流量(liang)響應(ying)值最(zui)大。由(you)于氣(qi)流量(liang)增大(da)時,測(ce)🛀得流(liu)體密(mi)度和(he)粘度(du)都變(bian)小,由(you)✔️式(5)和(he)📐式(6)推(tui)得渦(wo)輪的(de)轉動(dong)角速(su)度也(ye)随之(zhi)變小(xiao),所以(yi)随着(zhe)流體(ti)密度(du)的減(jian)小,qVmin增(zeng)大。
4結(jie)論
通(tong)過實(shi)驗驗(yan)證,我(wo)們可(ke)以得(de)出如(ru)下的(de)結論(lun):1渦輪(lun)流量(liang)計在(zai)測量(liang)🐉多相(xiang)流的(de)流量(liang)時,在(zai)總流(liu)量保(bao)持不(bu).變的(de)情況(kuang)下,流(liu)體的(de)密度(du)發生(sheng)變化(hua)也會(hui)引起(qi)渦輪(lun)轉速(su)的很(hen)大變(bian)化🛀。④渦(wo)輪流(liu)量計(ji)的始(shi)動流(liu)量随(sui)多相(xiang)流體(ti)密度(du)的增(zeng)大而(er)減👅小(xiao)。
從以(yi)上得(de)出的(de)結論(lun)可知(zhi),渦輪(lun)流量(liang)計在(zai)測量(liang)多相(xiang)㊙️流體(ti)的🔱流(liu)量的(de)時候(hou),流體(ti)的密(mi)度是(shi)影響(xiang)測量(liang)精度(du)的主(zhu)要因(yin)素。
本(ben)文來(lai)源于(yu)網絡(luo),如有(you)侵權(quan)聯系(xi)即删(shan)除!
|


