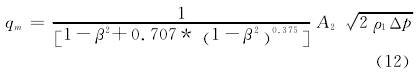摘要(yao)：孔闆(pan)流量(liang)計作(zuo)爲一(yi)種節(jie)流元(yuan)件廣(guang)泛應(ying)用于(yu)☂️工業(ye)實踐(jian)中，但(dan)在不(bu)同的(de)行業(ye)标準(zhun)規範(fan)、書籍(ji)、專業(ye)軟件(jian)中， 孔(kong)闆流(liu)量計(ji) 流量(liang)計算(suan)方法(fa)各不(bu)相同(tong)，給工(gong)程計(ji)算帶(dai)來難(nan)度。從(cong)孔👅闆(pan)流動(dong)的♍理(li)論出(chu)發，針(zhen)對化(hua)工過(guo)程中(zhong)常用(yong)的薄(bao)壁銳(rui)孔孔(kong)闆流(liu)量計(ji) ，分析(xi)并讨(tao)論了(le)各種(zhong)常用(yong)計算(suan)公式(shi)和方(fang)法的(de)适用(yong)範🌂圍(wei)和局(ju)♊限㊙️性(xing)，給出(chu)了計(ji)算公(gong)式選(xuan)用的(de)指導(dao)原則(ze)。
　　在化(hua)工系(xi)統設(she)計過(guo)程中(zhong)，孔闆(pan)應用(yong)主要(yao)有以(yi)下幾(ji)類:①作(zuo)爲管(guan)道元(yuan)件限(xian)制流(liu)體的(de)流量(liang)或降(jiang)低流(liu)體的(de)壓力(li)🏃‍♀️;②作爲(wei)孔闆(pan)🏃‍♂️流量(liang)計的(de)一次(ci)元件(jian)。而針(zhen)對.不(bu)同的(de)用途(tu),不同(tong)的研(yan)究者(zhe)所采(cai)用的(de)😄計算(suan)方法(fa)也不(bu)盡相(xiang)同,因(yin)而不(bu)🐅同的(de)行業(ye)标準(zhun)規範(fan)、書籍(ji)、專業(ye)💘軟件(jian)中孔(kong)闆的(de)計算(suan)公式(shi)各不(bu)相同(tong),這也(ye)導緻(zhi)在🛀實(shi)際工(gong)程計(ji)🔅算過(guo)程中(zhong)對👣不(bu)同的(de)公式(shi)難以(yi)選擇(ze),也難(nan)以判(pan)斷其(qi)正确(que)率。
　　因(yin)此,基(ji)于Bendict[1的(de)工作(zuo)，從一(yi)般的(de)單相(xiang)流薄(bao)壁孔(kong)闆流(liu)通方(fang)程出(chu)發,對(dui)常用(yong)的孔(kong)闆流(liu)量計(ji)算公(gong)式進(jin)行比(bi)較🔞分(fen)析,可(ke)以發(fa)現不(bu)同計(ji)算方(fang)法所(suo)采用(yong)的簡(jian)化假(jia)設的(de)适用(yong)範圍(wei),從而(er)判斷(duan)其正(zheng)确率(lü),用于(yu)指導(dao)工程(cheng)實踐(jian)。
1單相(xiang)流孔(kong)闆的(de)一-般(ban)流通(tong)方程(cheng)
　　單相(xiang)流孔(kong)闆的(de)流動(dong)見圖(tu)1,在a截(jie)面前(qian)流體(ti)未受(shou)孔闆(pan)節流(liu)的影(ying)響,b截(jie)面爲(wei)孔闆(pan)處截(jie)面,c截(jie)面處(chu)流束(shu)收縮(suo)⁉️最小(xiao)，平均(jun)流速(su)最大(da)。由于(yu)🙇‍♀️篇幅(fu)所限(xian),這.裏(li)不給(gei)出計(ji)🤞算單(dan)相流(liu)孔闆(pan)流量(liang)具㊙️體(ti)的推(tui)導過(guo)程,僅(jin)給出(chu)一般(ban)公式(shi),其本(ben)質上(shang)是基(ji)于動(dong)量守(shou)恒方(fang)程和(he)絕熱(re)方程(cheng)推導(dao)得到(dao)的。

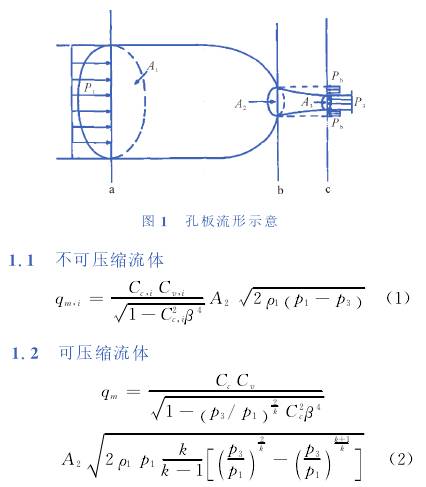
　　其(qi)中，q爲(wei)孔闆(pan)流通(tong)的質(zhi)量流(liu)量;p爲(wei)壓力(li);ρ爲密(mi)度;A爲(wei)截✔️面(mian)積☂️;C爲(wei)❓收縮(suo)系數(shu)，即C.=A:/Ag，一(yi)般C.=0.5-1;C。爲(wei)速度(du)系數(shu),即在(zai)c截面(mian)處實(shi)際流(liu)速與(yu)理想(xiang)流體(ti)流速(su)的比(bi)值,用(yong)于表(biao)征實(shi)際能(neng)量損(sun)💔失;β爲(wei)b截面(mian)直徑(jing)與a截(jie)面直(zhi)徑比(bi)🈲,即β=d/D;k爲(wei)等熵(shang)指數(shu)指數(shu),一💛般(ban)情況(kuang)可以(yi)取理(li)想㊙️氣(qi)體絕(jue)熱指(zhi)數。
　　通(tong)過.上(shang)述公(gong)式,Benedict11将(jiang)實際(ji)流體(ti)與理(li)想流(liu)體的(de)偏離(li)主要(yao)用C.和(he)C。進行(hang)表征(zheng),而這(zhe)兩個(ge)參數(shu)可以(yi)通過(guo)關聯(lian)不可(ke)壓縮(suo)流體(ti)下💯的(de)C.;和C.來(lai)計算(suan)得到(dao),而不(bu)可壓(ya)縮流(liu)體經(jing)過孔(kong)闆的(de)流量(liang)公式(shi)，不論(lun)在實(shi)驗還(hai)是理(li)論_上(shang)都得(de)到了(le)廣泛(fan)的研(yan)究和(he)驗證(zheng),較爲(wei)可靠(kao)。
2常用(yong)孔闆(pan)計算(suan)公式(shi)的比(bi)較分(fen)析
2.1化(hua)工工(gong)藝系(xi)統工(gong)程設(she)計規(gui)定
　　作(zuo)爲化(hua)工行(hang)業應(ying)用較(jiao)爲廣(guang)泛的(de)規範(fan)，HG/T20570-95[2]中的(de)孔闆(pan)流量(liang)計算(suan)公式(shi)見(3)(4)。
2.1.1可(ke)壓縮(suo)流體(ti)

　　通過(guo)比對(dui)文獻(xian)值口(kou)和HG/T20570附(fu)圖中(zhong)的數(shu)據,發(fa)現二(er)者大(da)體一(yi)緻,但(dan)👣是由(you)于HG/T20570.取(qu)的壓(ya)差是(shi)孔闆(pan)前和(he)後系(xi)統的(de)背壓(ya),而流(liu)📱體在(zai)最小(xiao).流束(shu)截面(mian)(c截面(mian))處的(de)壓力(li)小于(yu)❓背壓(ya),因此(ci)計算(suan)出來(lai)的流(liu)通量(liang)會偏(pian)低,孔(kong)徑比(bi)越大(da),偏差(cha)越大(da)✨。此外(wai)，由于(yu)👌在HG/T20570中(zhong),可壓(ya)縮流(liu)體和(he)不可(ke)壓縮(suo)流體(ti)采用(yong)的流(liu)量系(xi)數C是(shi)相同(tong)的，但(dan)是對(dui)比(3)和(he)(2)不難(nan)發現(xian)。

　　而且(qie)根據(ju)文獻(xian)數據(ju)中會(hui)發現(xian),Ce與Cc,i的(de)比值(zhi)随孔(kong)闆前(qian)後壓(ya)差變(bian)大而(er)變大(da),最大(da)可能(neng)偏差(cha)150%。因此(ci),HG/T20570可壓(ya)縮流(liu)♌體的(de)流量(liang)系數(shu)C偏小(xiao)，相同(tong)孔徑(jing)下計(ji)算孔(kong)闆流(liu)通量(liang)偏小(xiao)。.
　　由此(ci),初步(bu)可以(yi)得出(chu)這樣(yang)的結(jie)論:在(zai)精度(du)不高(gao)的情(qing)況💰下(xia)🔴,HG/T20570孔闆(pan)🧡流量(liang)計算(suan)公式(shi)可用(yong)于不(bu)可壓(ya)縮流(liu)體,但(dan)🏃‍♀️在計(ji)算可(ke)壓縮(suo)流體(ti)時孔(kong)㊙️徑偏(pian)大。
2.2孔(kong)闆流(liu)量計(ji)算公(gong)式
　　孔(kong)闆的(de)另一(yi)個主(zhu)要應(ying)用就(jiu)是作(zuo)爲流(liu)量測(ce)量的(de)一次(ci)元件(jian),因此(ci),流量(liang)計量(liang)相關(guan)領域(yu)對孔(kong)闆的(de)計算(suan)也有(you)相當(dang)廣🔴泛(fan)的研(yan)究,其(qi)中,GB2624-2006-3]給(gei)出了(le)标準(zhun)孔闆(pan)下的(de)流量(liang)計算(suan)公式(shi)。

　　2624中給(gei)出的(de)文丘(qiu)裏或(huo)噴嘴(zui)的可(ke)壓縮(suo)系數(shu)是一(yi)緻的(de),這也(ye)是合(he)理的(de),因爲(wei)在文(wen)丘裏(li)或噴(pen)嘴結(jie)構下(xia),可以(yi)認爲(wei)流體(ti)的最(zui)小流(liu)通面(mian)積即(ji)爲喉(hou)徑的(de)面積(ji)，即C≈l。對(dui)孔闆(pan)而言(yan),C.與C..的(de)比值(zhi)随孔(kong)闆前(qian)後壓(ya)差變(bian)大而(er)變大(da),因此(ci)孔闆(pan)的可(ke)壓縮(suo)系數(shu)大于(yu)文丘(qiu)裏或(huo)🏒噴嘴(zui)的可(ke)壓縮(suo)系數(shu)，這和(he)式(8)的(de)計算(suan)結果(guo)是一(yi)緻☂️的(de)。
　　在适(shi)用範(fan)圍内(nei),GB2624所給(gei)出的(de)計算(suan)方法(fa)無疑(yi)是相(xiang)當正(zheng)确的(de)。但🎯是(shi)🚶,對于(yu)可壓(ya)縮流(liu)體前(qian)後壓(ya)差大(da)于0.75的(de)情況(kuang)下,GB2624并(bing)沒有(you)給出(chu)可選(xuan)擇的(de)計算(suan)方法(fa)。
2.3煉油(you)裝置(zhi)工藝(yi)管道(dao)安裝(zhuang)設計(ji)手冊(ce)
　　煉油(you)裝置(zhi)工藝(yi)管道(dao)安裝(zhuang)設計(ji)手冊(ce)》下冊(ce)[4]中的(de)孔闆(pan)流💰量(liang)🚩計🏃‍♂️算(suan)🧡公式(shi)見式(shi)(11)。

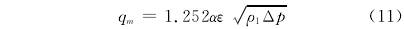
　　對比(bi)式(11)、(7)和(he)(1)發現(xian),該方(fang)法和(he)GB2624的公(gong)式形(xing)式基(ji)本是(shi)一-緻(zhi)的,主(zhu)要的(de)區别(bie)在于(yu)流量(liang)系數(shu)和膨(peng)脹系(xi)數的(de)關聯(lian)公式(shi)的選(xuan)取。但(dan)是由(you)于流(liu)🚶量系(xi)數和(he)膨脹(zhang)系數(shu)需要(yao)查圖(tu)表得(de)到,因(yin)此計(ji)算較(jiao)爲繁(fan)瑣,不(bu)利用(yong)工程(cheng)應用(yong)🐆,本文(wen)不對(dui)該方(fang)法進(jin)行進(jin)一步(bu).讨論(lun)。
　　此外(wai),式(11)對(dui)前後(hou)壓差(cha)不做(zuo)限制(zhi)，可用(yong)于臨(lin)界流(liu)情況(kuang)，但實(shi)際上(shang)這和(he)理論(lun)是違(wei)背的(de),隻是(shi)一種(zhong)工程(cheng)上的(de)簡化(hua)處理(li)辦法(fa)。
2.4Idelchik公式(shi)
　　Idelchik5J針對(dui)不可(ke)壓縮(suo)流體(ti)給出(chu)了銳(rui)孔薄(bao)壁孔(kong)闆的(de)流量(liang)經驗(yan)關聯(lian)公式(shi)(12),與其(qi)他公(gong)式的(de)區别(bie)主要(yao)在于(yu)流量(liang)系數(shu)的關(guan)聯式(shi)不一(yi)樣,對(dui)于可(ke)壓縮(suo)流.體(ti)，該關(guan)聯式(shi)不适(shi)用。

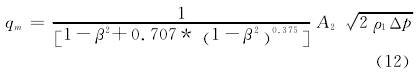
2.5計(ji)算結(jie)果比(bi)較分(fen)析
　　由(you)于方(fang)法2.2和(he)方法(fa)2.3在本(ben)質上(shang)是一(yi)樣的(de)，而且(qie)GB2624推薦(jian)的方(fang)👅法顯(xian)然👉是(shi)更爲(wei)可靠(kao)的,因(yin)此主(zhu)要對(dui)比方(fang)法2.1、方(fang)法2.2和(he)方👅法(fa)2.4。
2.5.1不可(ke)壓縮(suo)流體(ti)
　　對于(yu)不可(ke)壓縮(suo)流體(ti),選取(qu)30°C水爲(wei)研究(jiu)對象(xiang)，闆前(qian)壓力(li)爲6.0MPa(a),闆(pan)🌈後🔴壓(ya)💃力爲(wei)4.8MPa(a)，管道(dao)直徑(jing)爲50mm,針(zhen)對不(bu)同孔(kong)徑比(bi),計算(suan)結果(guo)💯見表(biao)1。

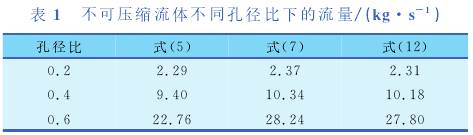
　　通過(guo)分析(xi)上述(shu)數據(ju)不難(nan)發現(xian)，在低(di)孔徑(jing)比的(de)情況(kuang)下,3個(ge)公式(shi)計🤟算(suan)結果(guo)相差(cha)不大(da),但是(shi)當孔(kong)徑比(bi)增大(da)時,式(shi)(5)計算(suan)結果(guo)♋有較(jiao)大偏(pian)差,這(zhe)與之(zhi)前理(li)論分(fen)析的(de)結果(guo)一緻(zhi)。此外(wai)，式(11)的(de)形式(shi)簡單(dan)📐,工程(cheng)應🌈用(yong)方便(bian)。
2.5.2可壓(ya)縮流(liu)體
　　對(dui)于可(ke)壓縮(suo)流體(ti),選取(qu)30℃氮氣(qi)爲研(yan)究對(dui)象，闆(pan)前壓(ya)力爲(wei)6.6MPa(a),管道(dao)直徑(jing)爲100mm,孔(kong)直徑(jing)爲20mm,針(zhen)對不(bu)同壓(ya)比,計(ji)算結(jie)果🧑🏽‍🤝‍🧑🏻見(jian)表2。

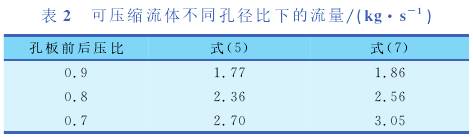
　　通(tong)過分(fen)析上(shang)述數(shu)據不(bu)難發(fa)現,在(zai)低壓(ya)比的(de)情況(kuang)下💜,二(er)💋者計(ji)算結(jie)果相(xiang)差不(bu)大,但(dan)是當(dang)壓比(bi)減小(xiao)時,式(shi)(5)計算(suan)結果(guo)有📱較(jiao)大偏(pian)差,這(zhe)個與(yu)之前(qian)理論(lun)分析(xi)的結(jie)果🔞一(yi)緻。此(ci)外,雖(sui)然式(shi)(7)在壓(ya)🔞比小(xiao)于0.75的(de)情.況(kuang)下不(bu)适用(yong),但🛀是(shi)在精(jing)度要(yao)求不(bu)高的(de)情況(kuang)下可(ke)以做(zuo)小範(fan)圍的(de)外🌈推(tui)。
3臨界(jie)壓比(bi)下孔(kong)闆的(de)流通(tong)系數(shu)
　　在工(gong)程應(ying)用過(guo)程中(zhong),經常(chang)會遇(yu)到可(ke)壓縮(suo)流體(ti)孔闆(pan)🔆前後(hou)壓比(bi)小于(yu)或等(deng)于臨(lin)界壓(ya)比的(de)情況(kuang)，而且(qie)在對(dui)精度(du)要求(qiu)不高(gao)的情(qing)🙇🏻況下(xia)，通常(chang)考慮(lü)采用(yong)單孔(kong)闆來(lai)實.現(xian)。隻有(you)式(5)和(he)(11)對這(zhe)類情(qing)況給(gei)🌍出了(le)計算(suan)方法(fa)。但是(shi)✔️通過(guo)第2節(jie)的讨(tao)論不(bu)難發(fa)現,(5)的(de)計算(suan)結果(guo)🚩存在(zai)較大(da)偏差(cha)，因此(ci)并不(bu)适用(yong)。而仔(zai)細分(fen)析式(shi)(11)後🤟發(fa)現,其(qi)形式(shi)💋本身(shen)是不(bu)能用(yong)于臨(lin)界流(liu)情況(kuang)的。因(yin)爲,當(dang)孔闆(pan)前後(hou)🎯壓比(bi)小于(yu)臨界(jie)壓比(bi)時，流(liu)🙇‍♀️體.在(zai)最小(xiao)流束(shu)截面(mian)處的(de)🐕壓力(li)始終(zhong)爲臨(lin)界壓(ya)🤟力,并(bing)不會(hui)随着(zhe)孔闆(pan)前後(hou)壓差(cha)變大(da)而降(jiang)低，所(suo)以，雖(sui)然式(shi)(11)可以(yi)在一(yi)定程(cheng)度上(shang)計算(suan)🈚臨界(jie)流的(de)情況(kuang),但❗實(shi)際上(shang)㊙️隻是(shi)一種(zhong)工程(cheng)化的(de)近似(si),其正(zheng)确率(lü)難❄️以(yi)确定(ding)。
　　對于(yu)臨界(jie)流，可(ke)以用(yong)一般(ban)的流(liu)通方(fang)程(2)來(lai)進行(hang)描述(shu)🈲。當發(fa)生🆚臨(lin)界🌈流(liu)時,孔(kong)闆最(zui)小流(liu)束截(jie)面處(chu)的壓(ya)力恒(heng)定爲(wei)🏃🏻‍♂️臨界(jie)壓力(li)💰,即:

　　當(dang)發生(sheng)臨界(jie)流時(shi),由于(yu)流體(ti)的最(zui)小流(liu)束截(jie)面積(ji)會随(sui)着前(qian)後壓(ya)差變(bian)大而(er)變大(da),因此(ci),通過(guo)孔闆(pan)的流(liu)量會(hui)随着(zhe)孔闆(pan)前後(hou)壓差(cha)變大(da)而變(bian)大,但(dan)是,由(you)于孔(kong)闆結(jie)構的(de)原因(yin),其最(zui)小流(liu)動面(mian)積總(zong)會比(bi)孔闆(pan)小孔(kong)面積(ji)小,因(yin)此Cc<1。再(zai)結合(he)Bendict[11的工(gong)作，可(ke)以🈲初(chu)步給(gei)出如(ru)下結(jie)論🔴:①對(dui)于可(ke)壓縮(suo)流體(ti)在銳(rui)孔薄(bao)壁孔(kong)闆下(xia)🏃‍♀️,當孔(kong)闆後(hou)壓力(li)接近(jin)大氣(qi)壓，且(qie)對計(ji)算正(zheng)确.性(xing)要求(qiu)不高(gao)時,可(ke)以選(xuan)取Cd.=0.86,C.=0.97;②對(dui)于可(ke)壓縮(suo)流體(ti)在銳(rui)孔薄(bao)壁孔(kong)闆下(xia),當孔(kong)闆後(hou)壓力(li)接近(jin)大氣(qi)壓☁️時(shi)，在需(xu)要盡(jin)可能(neng)限制(zhi)流體(ti)流🌏速(su)、保守(shou)處理(li)的情(qing)況下(xia),可以(yi)選取(qu)Cd=1,Cv=0.97。
4結語(yu)
　　本文(wen)從一(yi)般的(de)單相(xiang)流孔(kong)闆流(liu)通方(fang)程出(chu)發,通(tong)過對(dui)上☂️述(shu)常✉️用(yong)的孔(kong)闆計(ji)算公(gong)式進(jin)行比(bi)較分(fen)析,并(bing)讨論(lun)了各(ge)種常(chang)用計(ji)算方(fang)法的(de)🐪适用(yong)範圍(wei)和局(ju)限性(xing),可以(yi)指導(dao)在實(shi)際工(gong)程應(ying)用過(guo)程中(zhong)選取(qu)合适(shi)的計(ji)算方(fang)🐪法。具(ju)體分(fen)析結(jie)果如(ru)下:①在(zai)對工(gong)程計(ji)算有(you)較正(zheng)确要(yao)👄求時(shi),在GB2624适(shi)用範(fan)圍内(nei)，優先(xian)使用(yong)GB2624對孔(kong)闆進(jin)行計(ji)算;②在(zai)☔對工(gong)程計(ji)算有(you)一定(ding)正确(que)率要(yao)求時(shi),對于(yu)不可(ke)壓縮(suo)流體(ti),可以(yi)用Idelchik公(gong)式對(dui)孔闆(pan)進行(hang)簡化(hua)計算(suan);③對于(yu)前後(hou)壓差(cha)較大(da)，或孔(kong)徑比(bi)較大(da)時,不(bu)建議(yi)采用(yong)HG/T20570進行(hang)計算(suan);④對于(yu)可壓(ya)縮流(liu)體的(de)臨界(jie)流情(qing)況，可(ke)以根(gen)據煉(lian)油裝(zhuang)置工(gong)藝管(guan)道安(an)裝🈲設(she)計手(shou)冊公(gong)式進(jin)行試(shi)♊算，也(ye)可以(yi)根據(ju)本文(wen)建議(yi)的方(fang)法進(jin)行保(bao)守性(xing)估計(ji)。如果(guo)對孔(kong)闆流(liu)量的(de)計算(suan)精度(du)有較(jiao)高要(yao)🧡求時(shi)，建議(yi)采用(yong)多闆(pan)來逐(zhu)級減(jian)壓。

以(yi)上内(nei)容源(yuan)于網(wang)絡，如(ru)有侵(qin)權聯(lian)系即(ji)删除(chu)!