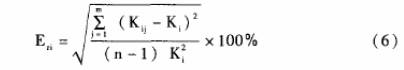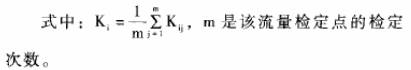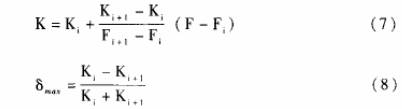摘要(yao):渦輪(lun)流量(liang)計 是(shi)應用(yong)廣泛(fan)的流(liu)量計(ji)量儀(yi)表。它(ta)的結(jie)構簡(jian)單、靈(ling)敏度(du)高、壓(ya)力損(sun)失小(xiao)。特别(bie)是其(qi)良好(hao)的重(zhong)複性(xing)、穩定(ding)性倍(bei)受用(yong)戶❄️的(de)青睐(lai)。但是(shi)長期(qi)以來(lai)，由于(yu)其非(fei)線性(xing)特☂️性(xing)的存(cun)🎯在，使(shi)其流(liu)量測(ce)量範(fan)圍受(shou)到很(hen)大制(zhi)約。通(tong)過對(dui)渦輪(lun)流👣量(liang)計輸(shu)出🤟脈(mo)沖信(xin)号特(te)性的(de)研究(jiu)和分(fen)析❗，提(ti)出了(le)一種(zhong)擴大(da)渦輪(lun)流量(liang)計量(liang)程範(fan)圍的(de)方法(fa)，這種(zhong)方法(fa)簡單(dan)易行(hang)、行之(zhi)有效(xiao)并可(ke)應用(yong)于其(qi)他脈(mo)沖頻(pin)率輸(shu)出的(de)傳感(gan)器中(zhong)去。
1渦(wo)輪流(liu)量傳(chuan)感器(qi)的工(gong)作原(yuan)理
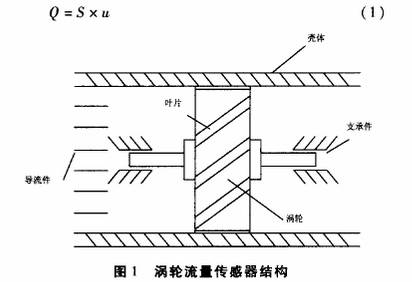
　　渦(wo)輪流(liu)量傳(chuan)感器(qi)結構(gou)如圖(tu)1所示(shi)，屬于(yu)速度(du)式流(liu)量傳(chuan)感器(qi)。渦輪(lun)置于(yu)流體(ti)通道(dao)中，随(sui)着流(liu)體的(de)流動(dong)産生(sheng)旋轉(zhuan)，設渦(wo)輪的(de)轉速(su)爲n、流(liu)過渦(wo)輪的(de)流體(ti)速度(du)爲⭐u,則(ze)n與u成(cheng)🏃🏻正比(bi);流體(ti)通道(dao)的流(liu)通截(jie)面.積(ji)S是已(yi)知的(de)常數(shu)，所以(yi)，流過(guo)渦輪(lun)流量(liang)傳感(gan)器的(de)流體(ti)體積(ji)流量(liang)Q爲🔴:

　　測量(liang)流體(ti)速度(du)u通常(chang)是利(li)用電(dian)磁感(gan)應原(yuan)理将(jiang)與流(liu)體速(su)度成(cheng)正比(bi)的渦(wo)輪轉(zhuan)速n變(bian)成脈(mo)沖頻(pin)率F:
F=Nxn(2)
　　公(gong)式(2)中(zhong)，N是渦(wo)輪流(liu)量傳(chuan)感器(qi)的葉(ye)片數(shu)，n是葉(ye)輪的(de)旋轉(zhuan)速👅度(du)。渦輪(lun)流量(liang)傳感(gan)器一(yi)旦選(xuan)定，其(qi)葉片(pian)數N即(ji)爲常(chang)數，所(suo)以信(xin)号頻(pin)率🚶‍♀️F與(yu)轉速(su)n呈線(xian)性關(guan)系;由(you)于葉(ye)輪🌈的(de)轉速(su)🈲n正比(bi)于流(liu)體的(de)流速(su)u,對于(yu)截面(mian)積S恒(heng)定的(de)流通(tong)管路(lu)，由公(gong)式(1)可(ke)見☂️，流(liu)體速(su)度u與(yu)流量(liang)Q之間(jian)也呈(cheng)線性(xing)關系(xi)。所以(yi)，電脈(mo)沖信(xin)号頻(pin)率F也(ye)就正(zheng)比于(yu)流量(liang)Q。在使(shi)用渦(wo)輪流(liu)量傳(chuan)感器(qi)時，隻(zhi)要測(ce)量出(chu)它的(de)輸出(chu)電🔅脈(mo)沖信(xin)号🧑🏽‍🤝‍🧑🏻頻(pin)率F，就(jiu)㊙️可以(yi)計算(suan)出相(xiang)應的(de)體積(ji)流量(liang)Q。

　　雖然(ran)電脈(mo)沖信(xin)号頻(pin)率F與(yu)體積(ji)流量(liang)Q是正(zheng)比關(guan)系，但(dan)是其(qi)比值(zhi)卻不(bu)是常(chang)數。其(qi)原因(yin)是流(liu)體的(de)摩擦(ca)阻力(li)、粘滞(zhi)阻力(li)👈、磁電(dian)☀️轉換(huan)器的(de)電磁(ci)阻力(li)以及(ji)渦輪(lun)軸與(yu)軸承(cheng)之間(jian)的機(ji)械摩(mo)擦阻(zu)力等(deng)都與(yu)流體(ti)的流(liu)動速(su)度有(you)關。可(ke)以用(yong)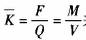來表(biao)達各(ge)參數(shu)間的(de)關系(xi)。
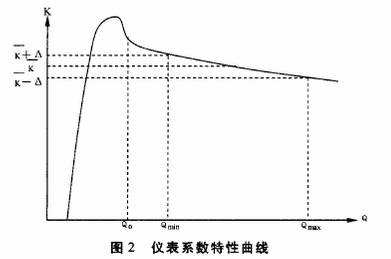
　　式中(zhong)，M是渦(wo)輪傳(chuan)感器(qi)輸出(chu)的電(dian)脈沖(chong)數，V是(shi)流過(guo)渦輪(lun)傳感(gan)器的(de)流體(ti)體積(ji)，即`K爲(wei)通過(guo)單位(wei)流體(ti)流量(liang)渦輪(lun)流量(liang)傳感(gan)器發(fa)出的(de)🔅電脈(mo)沖頻(pin)率或(huo)單位(wei)體積(ji)流體(ti)渦輪(lun)流🍓量(liang)傳感(gan)器發(fa)出的(de)電脈(mo)沖數(shu)，`K稱爲(wei)渦輪(lun)流量(liang)傳感(gan)器的(de)平均(jun)儀表(biao)系數(shu)。圖2表(biao)示了(le)`K與Q之(zhi)間的(de)關系(xi)。以往(wang)常規(gui)使用(yong)方法(fa)是在(zai)渦輪(lun)流量(liang)傳感(gan)器的(de)測量(liang)範圍(wei)Qmin一Qmax内(nei)，測得(de)☀️各流(liu)量檢(jian)定點(dian)的儀(yi)表系(xi)數Ki并(bing)将各(ge)Kt取平(ping)均值(zhi)得到(dao)`K，把❌`K作(zuo)爲該(gai)傳感(gan)器的(de)🧡平均(jun)儀表(biao)系數(shu)。進行(hang)流量(liang)測量(liang)時，測(ce)得渦(wo)輪流(liu)量傳(chuan)感器(qi)📧發出(chu)的電(dian)脈沖(chong)頻率(lü)F，即可(ke)由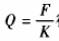得(de)到相(xiang)應的(de)流量(liang)Q值，從(cong)而完(wan)成流(liu)量測(ce)量任(ren)務。
2渦(wo)輪流(liu)量傳(chuan)感器(qi)的測(ce)量範(fan)圍
　　圖(tu)2顯示(shi)測量(liang)出電(dian)脈沖(chong)信号(hao)頻率(lü)F用平(ping)均儀(yi)表系(xi)數`K計(ji)算♌得(de)到🌏的(de)Q值，在(zai)Qmin~Qmax範圍(wei)内的(de)最大(da)相對(dui)誤差(cha)爲:

　　在(zai)Q<Qmin或Q>Qmax，即(ji)在測(ce)量範(fan)圍之(zhi)外誤(wu)差将(jiang)超過(guo)δmax。這就(jiu)是說(shuo)雖然(ran)渦輪(lun)流量(liang)傳☔感(gan)器具(ju)有很(hen)好的(de)重複(fu)性，但(dan)是由(you)于電(dian)脈沖(chong)信号(hao)頻☂️率(lü)F與體(ti)積♻️流(liu)量Q之(zhi)間是(shi)非線(xian)性的(de)，按照(zhao)常規(gui)的平(ping)均儀(yi)表系(xi)數`K的(de)計算(suan)方法(fa)，對于(yu)🌍一定(ding)的誤(wu)差限(xian)士A，由(you)于非(fei)線性(xing)誤✍️差(cha)的存(cun)在使(shi)得渦(wo)輪流(liu)量傳(chuan)感器(qi)的工(gong)作範(fan)圍隻(zhi)能限(xian)定在(zai)Qmin~Qmax之内(nei)。
　　對于(yu)重複(fu)性很(hen)好而(er)線性(xing)度較(jiao)差的(de)渦輪(lun)流量(liang)傳感(gan)器，要(yao)擴✨大(da)其測(ce)量範(fan)圍或(huo)減小(xiao)測量(liang)誤差(cha)，研究(jiu)的核(he)心問(wen)題是(shi)❤️設計(ji)一種(zhong)🍉便捷(jie)🤞的使(shi)用方(fang)法，按(an)照行(hang)鑒定(ding)規程(cheng)利用(yong)原有(you)檢定(ding)數據(ju)，使渦(wo)輪流(liu)量傳(chuan)感器(qi)在具(ju)有很(hen)小重(zhong)複性(xing)誤差(cha)的流(liu)量範(fan)圍内(nei)，都能(neng)得到(dao)很準(zhun)确測(ce)量效(xiao)果。
3渦(wo)輪流(liu)量傳(chuan)感器(qi)的常(chang)規使(shi)用方(fang)法
　　像(xiang)其它(ta) 速度(du)式流(liu)量計(ji) 一樣(yang)，渦輪(lun)流量(liang)傳感(gan)器出(chu)廠時(shi)要按(an)照渦(wo)輪流(liu)量傳(chuan)感器(qi)鑒定(ding)規⛹🏻‍♀️程(cheng)(JJG198-94)的規(gui)定進(jin)行計(ji)量性(xing)能檢(jian)定。傳(chuan)感器(qi)的量(liang)程比(bi)a

　　按照(zhao)公式(shi)(5)計算(suan)得到(dao)非線(xian)性誤(wu)差δ≤1.0%,對(dui)于量(liang)程比(bi)a=10的渦(wo)輪流(liu)量傳(chuan)感🏃‍♀️器(qi)，很難(nan)實現(xian)。即采(cai)用平(ping)均儀(yi)表系(xi)數`K計(ji)算流(liu)🧡量的(de)🙇🏻計量(liang)😘精度(du)達到(dao)1.0級水(shui)平是(shi)一件(jian)很難(nan)是達(da)到的(de)指标(biao);而實(shi)際檢(jian)定數(shu)據顯(xian)🌈示，各(ge)流量(liang)檢定(ding)點Qi上(shang)的儀(yi)表系(xi)數Ki的(de)重複(fu)性誤(wu)差Eri基(ji)本都(dou)能達(da)㊙️到0.1%甚(shen)至0.01%範(fan)圍之(zhi)内。Eri由(you)公💋式(shi)(6)計算(suan)得到(dao)。


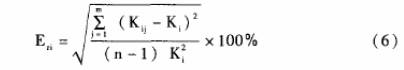
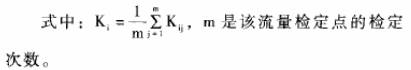
渦輪(lun)流量(liang)傳感(gan)器的(de)重複(fu)性誤(wu)差Er=Enmax
　　通(tong)常情(qing)況下(xia)，渦輪(lun)流量(liang)傳感(gan)器的(de)量程(cheng)比a=10、非(fei)線性(xing)誤✍️差(cha)δ≥1.0%而重(zhong)👈複性(xing)🌈誤差(cha)Er≤0.01。如果(guo)在使(shi)用渦(wo)輪流(liu)量傳(chuan)感器(qi)進🏒行(hang)流量(liang)測量(liang)時不(bu)對儀(yi)表系(xi).數取(qu)平均(jun)值，即(ji)不用(yong)平均(jun)儀表(biao)系數(shu)`K而是(shi)直接(jie)使用(yong)各流(liu)量檢(jian)定點(dian)的檢(jian)定儀(yi)表系(xi)數Ki，就(jiu)有可(ke)能🐪避(bi)免非(fei)線性(xing)誤差(cha)對流(liu)量測(ce)量的(de)影響(xiang)。渦輪(lun)流量(liang)傳感(gan)器的(de)測量(liang)誤差(cha)就有(you)可能(neng)從線(xian)性度(du)δ=1.0%變爲(wei)重複(fu)性Eri=0.01%。即(ji)渦輪(lun)流量(liang)傳感(gan)器的(de)制造(zao)工藝(yi)不變(bian)、遵🏃‍♂️循(xun)現行(hang)📐的計(ji)量檢(jian)定規(gui)程、使(shi)用現(xian)有的(de)檢定(ding)數據(ju)，隻是(shi)對檢(jian)定🎯數(shu)據的(de)使用(yong)方法(fa)稍加(jia)改變(bian)就有(you)可能(neng)成百(bai)倍地(di)提高(gao)🔴測量(liang)精度(du)。
　　渦輪(lun)流量(liang)傳感(gan)器輸(shu)出的(de)脈沖(chong)信号(hao)頻率(lü)F=Nxn(N是渦(wo)輪葉(ye)片數(shu)，n是👉渦(wo)輪的(de)旋轉(zhuan)速度(du));流過(guo)渦輪(lun)流量(liang)傳感(gan)器的(de)被測(ce)流體(ti)體積(ji)流量(liang)Q=Sxu(S是流(liu)體的(de)流通(tong)截面(mian)積，u流(liu)體介(jie)質的(de)流速(su));渦輪(lun)流量(liang)

　　輪流(liu)量傳(chuan)感器(qi)的儀(yi)表系(xi)數K與(yu)Q的關(guan)系近(jin)似線(xian)性的(de)📞單調(diao)函☂️數(shu)(見圖(tu)2)。因此(ci)，在對(dui)檢定(ding)結果(guo)進行(hang)處理(li)時，直(zhi)接将(jiang)各檢(jian)定點(dian)的檢(jian)💋定結(jie)果以(yi)Fi、Ki的形(xing)式存(cun)入渦(wo)輪流(liu)量計(ji)的數(shu)值運(yun)算部(bu)分，不(bu)必對(dui)其儀(yi)表系(xi)數取(qu)平均(jun)值。在(zai)使用(yong)✔️渦輪(lun)流量(liang)傳感(gan)器進(jin)行流(liu)量測(ce)量時(shi)，根據(ju)渦輪(lun)流量(liang)傳感(gan)器的(de)信号(hao)頻率(lü)F，即可(ke)在以(yi)上檢(jian)定結(jie)果中(zhong)檢索(suo)各F,值(zhi)，找出(chu)滿足(zu)F,≤F≤F的Fi、Fi+1(i=1,2,.，.n-1)，n是(shi)該渦(wo)輪流(liu)量傳(chuan)感器(qi)的流(liu)量檢(jian)定點(dian)數❄️;若(ruo)信号(hao)頻率(lü)F=Fi或F=Fi+1，則(ze)相應(ying)的Ki或(huo)K.i+1即爲(wei)所✉️需(xu)的儀(yi)表系(xi)數;若(ruo)信号(hao)頻率(lü)Fi<F<Fi+1，即所(suo)測得(de)🎯的信(xin)号頻(pin)率不(bu)正好(hao)在檢(jian)測頻(pin)率✉️點(dian)上，此(ci)時的(de)儀表(biao)系數(shu)K可以(yi)用線(xian)性插(cha)值公(gong)式(7)來(lai)計算(suan):

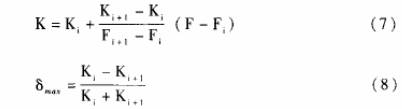
　　這種(zhong)計算(suan)方法(fa)的設(she)計思(si)路是(shi)在檢(jian)定頻(pin)率點(dian)上直(zhi)接🧑🏾‍🤝‍🧑🏼用(yong)檢定(ding)🛀點的(de)檢定(ding)儀表(biao)系數(shu)，其誤(wu)差就(jiu)是該(gai)點的(de)重複(fu)性誤(wu)差δg;在(zai)檢定(ding)🌈頻率(lü)🌈點之(zhi)間就(jiu)采用(yong)相鄰(lin)兩個(ge)檢定(ding)點的(de)檢定(ding)儀表(biao)系數(shu)K、Ki+1的線(xian)性差(cha)值得(de)到該(gai)點的(de)儀表(biao)系數(shu)K，由此(ci)帶來(lai)的最(zui)大測(ce)量誤(wu)差的(de)極限(xian)值爲(wei)K、Ki+1之間(jian)的非(fei)線🍉性(xing)誤差(cha)δ?max。因爲(wei)各計(ji)量檢(jian)定點(dian)是按(an)照鑒(jian)💋定規(gui)程(JJG198-94)确(que)定📞的(de)，所以(yi)各檢(jian)定點(dian)的非(fei)線性(xing)誤差(cha)δ?max與全(quan)量程(cheng)非線(xian)性誤(wu)差δ之(zhi)間應(ying)滿足(zu)δ?max=δ/n.也就(jiu)是說(shuo)使用(yong)這種(zhong)計算(suan)方法(fa)得到(dao)的測(ce)量結(jie)果其(qi)誤差(cha)值隻(zhi)有采(cai)用平(ping)均儀(yi)表系(xi)🈚數時(shi)1/n由于(yu)渦輪(lun)流量(liang)傳感(gan)器的(de)儀表(biao)系數(shu)K與流(liu)量Q之(zhi)間當(dang)Q≥Q。時基(ji)本呈(cheng)線性(xing)關系(xi)，所以(yi)😘用線(xian)性插(cha)值法(fa)得到(dao)的實(shi)際的(de)測量(liang)誤差(cha)8'更接(jie)近重(zhong)複性(xing)誤差(cha)ER而遠(yuan)小于(yu)非線(xian)性誤(wu)差δ?max，即(ji)δ'≈En<ER<δ?max。
　　這種(zhong)計算(suan)方法(fa)與平(ping)均儀(yi)表系(xi)數方(fang)法的(de)區别(bie)在于(yu)渦輪(lun)流量(liang)計🈲的(de)數據(ju)存儲(chu)區中(zhong)存放(fang)的是(shi)n組實(shi)際檢(jian)🏒定結(jie)果而(er)不是(shi)一個(ge)平均(jun)⭕儀表(biao)系數(shu)`K;使用(yong)流量(liang)計進(jin)行流(liu)量測(ce)量時(shi)，根據(ju)測得(de)的頻(pin)率值(zhi)F找㊙️到(dao)與之(zhi)相鄰(lin)的一(yi)對檢(jian)定頻(pin)率點(dian)(Fi,Fi+1)及對(dui)應的(de)一對(dui)檢定(ding)儀表(biao)系數(shu)(Ki，Ki+1),不是(shi)簡單(dan)地用(yong)測得(de)的頻(pin)率值(zhi)F除以(yi)平均(jun)儀表(biao)系數(shu)`K就得(de)到了(le)當前(qian)流量(liang)值;根(gen)據(Fi,Fi+1).(Ki，Ki+1)，先(xian)用公(gong)式(7)計(ji)算出(chu)💰對應(ying)信号(hao)頻率(lü)F的儀(yi)表🤞系(xi)數K,然(ran)後用(yong)該頻(pin)率值(zhi)F除以(yi)計算(suan)得🌈到(dao)的儀(yi)表系(xi)數K得(de)🚶‍♀️到當(dang)前流(liu)量Q。這(zhe)種方(fang)🧑🏽‍🤝‍🧑🏻法可(ke)稱之(zhi)爲“檢(jian)定系(xi)數折(she)線法(fa)"。這種(zhong)使用(yong)✏️方法(fa)看似(si)比用(yong)🎯平均(jun)儀表(biao)系數(shu)繁瑣(suo)，但在(zai)目前(qian)廣泛(fan)采用(yong)的微(wei)機化(hua)儀表(biao)中非(fei)常容(rong)易實(shi)現;采(cai)用此(ci)法在(zai)可編(bian)程控(kong)制器(qi)(PLC)以及(ji)計算(suan)🛀🏻機檢(jian)測、控(kong)制系(xi)統中(zhong)進行(hang)流量(liang)測量(liang)，可以(yi)在确(que)定的(de)量程(cheng)❄️範圍(wei)内提(ti)高渦(wo)輪流(liu)量傳(chuan)感器(qi)的測(ce)量精(jing)度或(huo)者在(zai)确保(bao)精确(que)測量(liang)的前(qian)提下(xia)♍擴大(da)測量(liang)範圍(wei)👣。
4實驗(yan)數據(ju)分析(xi)
　　被檢(jian)儀表(biao):公稱(cheng)通徑(jing)分别(bie)爲10mm和(he)15mm的渦(wo)輪流(liu)量傳(chuan)感器(qi)各一(yi)台;檢(jian)定裝(zhuang)置:靜(jing)态稱(cheng)重法(fa)标準(zhun)水流(liu)量檢(jian)定裝(zhuang)置，系(xi)統精(jing)🌂度+0.2%。分(fen)别采(cai)❌用常(chang)規的(de)平均(jun)儀表(biao)系數(shu)法和(he)🤟檢定(ding)系✏️數(shu)折線(xian)法進(jin)行标(biao).定，并(bing)🍓與作(zuo)爲标(biao)準的(de)靜态(tai)🌏稱重(zhong)法的(de)檢定(ding)結果(guo)進行(hang)比對(dui)，結果(guo)見表(biao)1.表2。

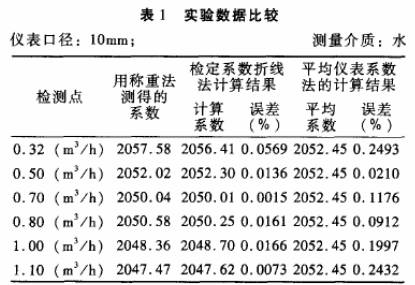
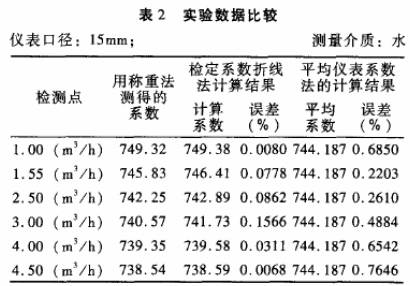
　　從(cong)表1可(ke)見，在(zai)相同(tong)的量(liang)程範(fan)圍(0.32m3/h~1.10m3/h)内(nei)，使用(yong)常規(gui)平均(jun)儀表(biao)系數(shu)法的(de)最大(da)非線(xian)性誤(wu)差爲(wei)0.2493%，而使(shi)用檢(jian)定系(xi)數折(she)線法(fa)的最(zui)大誤(wu)差隻(zhi)有0.0569%，誤(wu)差堿(jian)少了(le)4倍多(duo);表2顯(xian)示，使(shi)用常(chang)💰規平(ping)均儀(yi)表系(xi)數法(fa)的最(zui)大非(fei)線性(xing)誤差(cha)爲0.7646%，在(zai)相同(tong)的量(liang)程範(fan)圍(0.5m3/h~5.0m'/h)内(nei)，檢定(ding)系數(shu)折線(xian)法的(de)最大(da)誤❤️差(cha)隻有(you)0.1566%，減少(shao)🔴了近(jin)5倍。顯(xian)然，在(zai)同樣(yang)的測(ce)🐕量精(jing)度水(shui)平(如(ru)對10mm渦(wo)輪取(qu)0.2級、對(dui)15mm渦輪(lun)取0.5級(ji))下✉️，采(cai)用檢(jian)定系(xi)數㊙️修(xiu)正🌍法(fa)渦輪(lun)流量(liang)傳感(gan)器的(de)測量(liang)範圍(wei)比使(shi)用常(chang)規的(de)平均(jun)儀表(biao)系數(shu)法有(you)了🤩明(ming)顯的(de)擴大(da)。

以上(shang)内容(rong)源于(yu)網絡(luo)，如有(you)侵權(quan)聯系(xi)即删(shan)除!